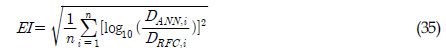1. ņä£ ļĪĀ
ņäĀļ░Ģ ļ░Å ĒĢ┤ņ¢æĒöīļ×£ĒŖĖļŖö ļŗżņ¢æĒĢ£ ĒÖśĻ▓ĮĒĢśņżæņ£╝ļĪ£ ņØĖĒĢ£ ļÅÖņĀüņÖĖļĀźņØä ļ│ĄĒĢ®ņĀüņ£╝ļĪ£ ļ░øņ£╝ļ®░ ņØ┤ļĪ£ ņØĖĒĢ┤ ĒĢ┤ļŗ╣ ĻĄ¼ņĪ░ļ¼╝ņØś ņØæļŗĄņØĆ ļÅÖņĀü Ļ┤æļīĆņŚŁ ņØæļŗĄņŖżĒÄÖĒŖĖļ¤╝ņØä ĒśĢņä▒ĒĢ£ļŗż. ņØ┤ļ¤¼ĒĢ£ ļÅÖņĀüņØæļŗĄņØĆ ĻĄ¼ņĪ░ļ¼╝ņØś Ēö╝ļĪ£ņłśļ¬ģņŚÉ ņ¦üņĀæņĀüņØĖ ņśüĒ¢źņØä ņŻ╝ĻĖ░ ļĢīļ¼ĖņŚÉ ļÅÖņĀü Ļ┤æļīĆņŚŁ ņØæļŗĄņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ņČöņĀĢĒĢśļŖö Ļ▓āņØĆ ĒĢ┤ļŗ╣ ĻĄ¼ņĪ░ļ¼╝ ņäżĻ│äņŚÉ ļ¦żņÜ░ ĒĢäņłśņĀüņØĖ ņÜöņåīļØ╝ ĒĢĀ ņłś ņ׳ļŗż.
ļÅÖņĀüņØæļŗĄņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØĆ ņŗ£Ļ░äņśüņŚŁļé┤ņŚÉņä£ ļĀłņØĖĒöīļĪ£ņÜ░ ņ¦æĻ│äļ▓Ģ(Rain-flow counting method)(
Matsuishi and Endo, 1968)ņØä ņé¼ņÜ®ĒĢśņŚ¼ ĻĄ¼ĒĢśļŖö Ļ▓āņØ┤ Ļ░Ćņן ņĀĢĒÖĢĒĢśĻ│Ā ĒĢ®ļ”¼ņĀüņØĖ ļ░®ļ▓ĢņØ┤ļéś ņāüļŗ╣ĒĢ£ Ļ│äņé░ļ╣äņÜ®ņØ┤ ņåīņÜöļÉśņ¢┤ ļ╣äĒÜ©ņ£©ņĀüņØ┤ļŗż. ņØ┤ņÖĆ ļŗ¼ļ”¼ ņŻ╝ĒīīņłśņśüņŚŁņŚÉņä£ ņØæļŗĄ ņŖżĒÄÖĒŖĖļ¤╝ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśļŖö Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØĆ Ļ│äņé░ļ╣äņÜ®ņØ┤ ļ¦żņÜ░ ņĀüņ¢┤ ĒÜ©ņ£©ņĀüņØ┤ļéś Ēö╝ļĪ£ņåÉņāüņśłņĖĪ Ļ▓░Ļ│╝ņØś ņŗĀļó░ņä▒ņŚÉ ļīĆĒĢ£ Ļ▓ĆĒåĀĻ░Ć ņłśĒ¢ēļÉśņ¢┤ņĢ╝ ĒĢ£ļŗż. ņØ┤ ļĢīļ¼ĖņŚÉ ĒĢ®ļ”¼ņĀüņØĖ Ēö╝ļĪ£ņåÉņāüņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢ£ Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśĻĖ░ ņ£äĒĢ£ ņŚ░ĻĄ¼ļōżņØ┤ ļ¦ÄņØ┤ ņłśĒ¢ēļÉśņ¢┤ņĀĖ ņÖöļŗż. Wirsching-Light ļ¬©ļŹĖ(
Wirsching and Light, 1980)ņØĆ ļŗ©ņł£ĒĢśĻ│Ā ņĢĮĒĢ£ Ļ┤æļīĆņŚŁ ņØæļŗĄņŚÉ Ļ┤ĆĒĢ£ ĒĢ®ļ”¼ņĀüņØĖ Ļ░ÆņØä ņŻ╝ļ®░ ņäĀļ░Ģ ļ░Å ĒĢ┤ņ¢æĒöīļ×£ĒŖĖņØś ņÖäņĀäĒåĄĻ│äĒö╝ļĪ£ĒĢ┤ņäØņŚÉ ņŻ╝ļĪ£ ņØ┤ņÜ®ļÉśĻ│Ā ņ׳ņ£╝ļ®░, Dirlik ļ¬©ļŹĖ(
Dirlik, 1985)ņØĆ ĒĢ®ļ”¼ņĀüņØĖ ņØæļĀźļ▓öņ£äļČäĒżļź╝ ņĀ£Ļ│ĄĒĢśņŚ¼ Ļ┤æļīĆņŚŁ ņØæļŗĄņŚÉ ļīĆĒĢ┤ņä£ ĒĢ®ļ”¼ņĀüņØ┤ļéś ļŗżņåī Ļ│╝ņåīĒÅēĻ░ĆļÉśļŖö Ēö╝ļĪ£ņåÉņāüņØä ņżĆļŗż. Benasciutti-Tovo ļ¬©ļŹĖ(
Benasciutti and Tovo, 2005)ņØĆ ņłśņ╣śņŗżĒŚś ļ░Å Ļ▓ĮĒŚśņĀüņ£╝ļĪ£ ņ¢╗ņØĆ ņłśņĀĢĻ│äņłśļź╝ ņé¼ņÜ®ĒĢśņŚ¼ ļ¦żņÜ░ ņĀĢĒÖĢĒĢ£ Ēö╝ļĪ£ņåÉņāü ņČöņĀĢņ╣śļź╝ ņĀ£Ļ│ĄĒĢ┤ņŻ╝ļéś Ēö╝ļĪ£ņåÉņāüņØä Ļ│äņé░ĒĢśĻĖ░ ņ£äĒĢ┤ ņØ┤ļōżņØ┤ ņĀ£ņĢłĒĢ£ ņØæļĀźļ▓öņ£äļČäĒżļŖö ņŗżņĀ£ ļČäĒżņÖĆ ļ¦żņÜ░ ņāüņØ┤ĒĢ£ Ļ▓░Ļ│╝ļź╝ ļéśĒāĆļéĖļŗż(
Park, 2011). JBļ¬©ļŹĖ(
Park et al., 2014)ņØĆ Ļ┤æļīĆņŚŁ ņØæļŗĄņŚÉ ļīĆĒĢśņŚ¼ ņāüļīĆņĀüņ£╝ļĪ£ ņĀĢĒÖĢĒĢ£ Ēö╝ļĪ£ņåÉņāüĻ│╝ ņØæļĀźļ▓öņ£äļČäĒżļź╝ ņĀ£Ļ│ĄĒĢśļŖö ļ¬©ļŹĖņØ┤ļ®░ ņäĀļ░ĢņØś ņ£ĀĒāäņä▒ĒÜ©Ļ│╝ļĪ£ ņØĖĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśļŖöļŹ░ ņČöņ▓£ļÉ£ ļ¬©ļŹĖņØ┤ļŗż(
Lloyd's Register, 2014). ļśÉĒĢ£ ņé╝ļ┤ēĒśĢ Ļ┤æļīĆņŚŁ ņØæļŗĄņŚÉ ļīĆĒĢ┤ņä£ļÅä ĒĢ®ļ”¼ņĀüņØĖ Ēö╝ļĪ£ņåÉņāü Ļ░ÆņØä ņŻ╝ļŖö Ļ▓āņ£╝ļĪ£ ņĢīļĀżņĀĖ ņ׳ņ£╝ļéś(
Park and Song, 2015), ļ¦ÄņØĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│Ćņłś(Bandwidth parameter)ļź╝ ĻĄ¼ĒĢ┤ņĢ╝ ĒĢśļŖö ļŗ©ņĀÉņØ┤ ņ׳ļŗż.
ņĄ£ĻĘ╝ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä Ēö╝ļĪ£ņåÉņāüņŚÉ ņĀüņÜ®ĒĢśļŖö ņŚ░ĻĄ¼Ļ░Ć ņ¦äĒ¢ēļÉśņ¢┤ ņÖöļŗż(
Kang et al., 2013;
Kim et al., 2015). ņØ┤ļōżņØś ņŚ░ĻĄ¼ļŖö ļŗżņ¢æĒĢ£ ņŻ╝Ēīīņłś ļ▓öņ£äņŚÉ Ļ▒Ėņ│Éņä£ ļ»Ėļ”¼ ņĀĢņØśļÉ£ ņØæļŗĄņŖżĒÄÖĒŖĖļ¤╝ ĒśĢņāüņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ĒåĄĒĢśņŚ¼ ĒĢÖņŖĄĒĢ£ ĒøäņŚÉ, ĒĢÖņŖĄļÉśņ¦Ć ņĢŖņØĆ ļ╣äņŖĘĒĢ£ ĒśĢņāüņØś ņØæļŗĄņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢśņŚ¼ ļ¦żņÜ░ ņä▒Ļ│ĄņĀüņØĖ Ēö╝ļĪ£ņåÉņāü ņśłņĖĪĻ▓░Ļ│╝ļź╝ ļ│┤ņŚ¼ ņŻ╝ņŚłļŗż. ĒĢśņ¦Ćļ¦ī ļ│ĄĒĢ®ņĀüņØĖ ļÅÖņĀüņÖĖļĀźņŚÉ ņØśĒĢ£ ņŗżņĀ£ ņØæļŗĄņŖżĒÄÖĒŖĖļ¤╝ņØĆ ļ»Ėļ”¼ ņĀĢņØśļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ ĒśĢņāüņ£╝ļĪ£ ņĀüņÜ®ĒĢśĻĖ░ ņ¢┤ļĀĄĻĖ░ ļĢīļ¼ĖņŚÉ, ņŗżņĀ£ ņØæļŗĄņŖżĒÄÖĒŖĖļ¤╝ņØä ĒĢÖņŖĄļÉ£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņŚÉ ņĀüņÜ®ĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ ļ¦ÄņØĆ ņśżļźśļź╝ ļ░£ņāØņŗ£Ēé¼ ņłś ņ׳ļŖö ļŗ©ņĀÉņØ┤ ņ׳ļŗż. Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśņØś ĒĢ©ņłśļĪ£ Ēö╝ļĪ£ņåÉņāüņØś Ļ▓ĮĒ¢źņØä ņśłņĖĪĒĢśņśĆĻĖ░ ļĢīļ¼ĖņŚÉ ļģ╝ļ”¼ņāüņ£╝ļĪ£ ņ×äņØśņØś ĒśĢņāüņØś ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢśņŚ¼ ņĀüņÜ®ņØ┤ Ļ░ĆļŖźĒĢśļŗż. ļö░ļØ╝ņä£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ĒåĄĒĢśņŚ¼ ņ×äņØśņØś ĒśĢņāüņØä Ļ░Ćņ¦ĆļŖö ņØæļŗĄņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖĻ│╝ Ļ░ÖņØ┤ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśņÖĆ Ēö╝ļĪ£ņåÉņāüĻ│╝ņØś Ļ┤ĆĻ│äļź╝ ĒĢÖņŖĄĒĢ£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ĻĄ¼ņČĢĒĢśņŚ¼ņĢ╝ ĒĢ£ļŗż. ļśÉĒĢ£ ĻĄ¼ņČĢļÉ£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ĒåĄĒĢśņŚ¼ ņé¼ņÜ®ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ņØś ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżņØ┤ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśļŖöļŹ░ ņ¢╝ļ¦łļéś ņśüĒ¢źņØä ņŻ╝ļŖöņ¦ĆņŚÉ ļīĆĒĢ£ ļ»╝Ļ░ÉļÅäļÅä Ļ▓ĆĒåĀĒĢ┤ ļ│╝ ĒĢäņÜöĻ░Ć ņ׳ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĻĖ░ņĪ┤ņØś Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņŚÉ ļīĆĒĢśņŚ¼ ļČäņäØĒĢśĻ│Ā ņé¼ņÜ®ļÉ£ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśņÖĆ Ēö╝ļĪ£ņåÉņāüĻ│╝ņØś Ļ┤ĆĻ│äļź╝ ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņĀĢņØśĒĢ£ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ▓ĆĒåĀĒĢśĻ│Āņ×É ĒĢ£ļŗż. ļśÉĒĢ£ ņØĖĻ│Ą ņŗĀĻ▓Įļ¦ØņØä ņØ┤ņÜ®ĒĢ£ ļ»╝Ļ░ÉļÅä ĒĢ┤ņäØņØä ĒåĄĒĢśņŚ¼ ņ×äņØśņØś ĒśĢņāüņØś ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśļŖöļŹ░ ņĀüĒĢ®ĒĢ£ ņČöĻ░ĆņĀüņØĖ ļ¦żĻ░£ļ│Ćņłśļź╝ ņĀ£ņĢłĒĢśĻ│Āņ×É ĒĢ£ļŗż.
2. Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖ ļČäņäØ
2.1 ņŖżĒÄÖĒŖĖļ¤┤ ļ¬©ļ®śĒŖĖņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│Ćņłś
ļÅÖņĀüĒĢśņżæņŚÉ ļīĆĒĢ£ ņŖżĒÄÖĒŖĖļ¤╝ņØ┤
Fig. 1Ļ│╝ Ļ░ÖņØä ļĢī,
nņ░© ņŖżĒÄÖĒŖĖļ¤┤ ļ¬©ļ®śĒŖĖ(
mn)ļŖö ņŗØ (1)Ļ│╝ Ļ░ÖņØ┤ ņ×äņØśņØś ņŖżĒÄÖĒŖĖļ¤╝(
S(
Žē))Ļ│╝ ĒĢ┤ļŗ╣ ņ░©ņłśņØś ņŻ╝Ēīīņłś(
Žēn) Ļ│▒ņØä ņĀüļČäĒĢ£ Ļ▓āņØ┤ ļÉśļ®░, ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļŖö ņØ┤ļ¤¼ĒĢ£ ņŖżĒÄÖĒŖĖļ¤┤ ļ¬©ļ®śĒŖĖņØś ņĪ░ĒĢ®ņ£╝ļĪ£ ņŗØ (2)ņÖĆ Ļ░Öļŗż.
Fig.┬Ā1
Spectrum example
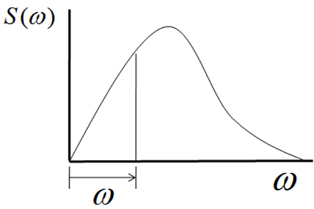
ņŖżĒÄÖĒŖĖļ¤╝ņØś ņśüņĀÉĻĄÉņ░©ņŻ╝ĻĖ░ņÖĆ Ēö╝Ēü¼ĻĄÉņ░©ņŻ╝ĻĖ░ļŖö ņŗØ (3)Ļ│╝ ņŗØ (4)ņÖĆ Ļ░ÖņØ┤ ņŖżĒÄÖĒŖĖļ¤┤ ļ¬©ļ®śĒŖĖļĪ£ ņ¢╗ņ¢┤ņ¦Ćļ®░, ņŖżĒÄÖĒŖĖļ¤╝ņØś ņśüņĀÉĻĄÉņ░©ņŻ╝ĻĖ░(Ø£ł0)ļŖö ņŗØ (5)ņÖĆ Ļ░ÖņØ┤ Ēö╝Ēü¼ĻĄÉņ░©ņŻ╝ĻĖ░(Ø£łp)ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśņØś Ļ│▒ņ£╝ļĪ£ Ēæ£ĒśäļÉ£ļŗż.
ņŗØ (1) ~ ņŗØ (5)ņŚÉņä£ ļ│┤ļŖöļ░öņÖĆ Ļ░ÖņØ┤ ņŖżĒÄÖĒŖĖļ¤┤ ļ¬©ļ®śĒŖĖļŖö ļÅÖņĀüĒĢśņżæņØś ĒŖ╣ņä▒ņØä ļéśĒāĆļé┤ļŖö ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│Ćņłś, ņśüņĀÉĻĄÉņ░©ņŻ╝ĻĖ░ņÖĆ Ēö╝Ēü¼ĻĄÉņ░©ņŻ╝ĻĖ░ņØś ņØĖņ×ÉļōżņØ┤ļ®░, ņØ┤ļŖö Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØś ņŻ╝ņÜöņØĖņ×ÉļĪ£ ĒÖ£ņÜ®ļÉ£ļŗż.
2.2 Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØś ļČäņäØ
Wirsching-Light ļ¬©ļŹĖņØĆ Ļ┤æļīĆņŚŁ ņØæļŗĄņ£╝ļĪ£ ņØĖĒĢ£ Ēö╝ļĪ£ņåÉņāüņØĆ ĒśæļīĆņŚŁ ņØæļŗĄņ£╝ļĪ£ ņØĖĒĢ£ Ēö╝ļĪ£ņåÉņāüņŚÉ ņłśņĀĢĻ│äņłśļź╝ Ļ│▒ĒĢ©ņ£╝ļĪ£ņŹ© ņ¢╗ņ¢┤ņ¦ĆļŖö Ļ▓āņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśņśĆņ£╝ļ®░, Wirsching-Light ļ¬©ļŹĖ Ēö╝ļĪ£ņåÉņāü(DWL)ņØĆ ņŗØ (6)Ļ│╝ Ļ░ÖņØ┤ ņĀ£ņĢłĒĢśņśĆļŗż.
ņŚ¼ĻĖ░ņä£ DNB ļŖö ņŗØ (7)Ļ│╝ Ļ░ÖņØ┤ ĒśæļīĆņŚŁ ņØæļŗĄņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØ┤ļ®░, ŽüWL ņØĆ ņłśņĀĢĻ│äņłśņØ┤ļ®░ ņŗØ (8), ņŗØ (9)ņÖĆ Ļ░ÖņØ┤ ņĀĢņØśĒĢśņśĆļŗż.
ņŚ¼ĻĖ░ņä£ TdļŖö ļÅÖņĀüņØæļŗĄņØ┤ ņ×æņÜ®ĒĢ£ ņŗ£Ļ░ä, mĻ│╝ CļŖö Ļ░üĻ░ü S-NņäĀļÅäņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ņłśļ¬ģņČĢ ņĀłĒÄĖņØ┤Ļ│Ā, ąō(ŌĆó) ļŖö Ļ░Éļ¦łĒĢ©ņłś(Gamma function)ņØ┤ļŗż.
ņŚ¼ĻĖ░ņä£
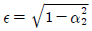
ņØ┤ļŗż.
ņŗØ (6)ņØä Ļ░äļŗ©Ē׳ Ēæ£ĒśäĒĢśļ®┤ ņŗØ (10)Ļ│╝ Ļ░ÖņØ┤ ņāüņłśĒĢŁ
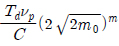
ņŚÉ S-NņäĀļÅäņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä ĒĢ©ņłś
fWL(ŌĆó)ņØ┤ Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.
Dirlik ļ¬©ļŹĖņØĆ ņØæļĀźļ▓öņ£äļČäĒżļź╝ ĻĘ╝ņé¼ĒĢśņŚ¼ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢ£ ļ¬©ļŹĖņØ┤ļŗż. Dirlik ļ¬©ļŹĖ Ēö╝ļĪ£ņåÉņāü(DDK)ņØĆ ņŗØ (11)Ļ│╝ Ļ░Öņ£╝ļ®░, ņØ┤ ļ¬©ļŹĖņŚÉ ņé¼ņÜ®ļÉ£ Ļ│äņłśļŖö ņŗØ (12) ~ ņŗØ (16)Ļ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£

ņØ┤ļŗż.
ņØ┤ ļ¬©ļŹĖļÅä Ļ░äļŗ©Ē׳ ņĀĢļ”¼ĒĢśļ®┤ ņŗØ (17)Ļ│╝ Ļ░ÖņØ┤ ņāüņłśĒĢŁ
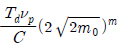
ņŚÉ
fDK(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£Ļ░Ć ļÉ£ļŗż.
Benasciutti-Tovo ļ¬©ļŹĖļÅä ņØæļĀźļ▓öņ£äļČäĒżļź╝ Ļ░ĆņĀĢĒĢśņŚ¼ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢ£ ļ¬©ļŹĖņØ┤ļ®░, Benasciutti-Tovo ļ¬©ļŹĖ Ēö╝ļĪ£ņåÉņāü(DBT)ņØĆ ņŗØ (18)Ļ│╝ Ļ░Öļŗż. ņØ┤ ļ¬©ļŹĖņŚÉ ņé¼ņÜ®ļÉ£ Ļ│äņłś(ŽüBT)ļŖö ņŗØ (19)ņÖĆ Ļ░Öļŗż.
ņØ┤ ļ¬©ļŹĖļÅä ņĀĢļ”¼ĒĢśļ®┤, ņŗØ (20)Ļ│╝ Ļ░ÖņØ┤ ņāüņłśĒĢŁ
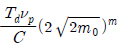
ņŚÉ
fBT(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.
JBļ¬©ļŹĖļÅä ņØæļĀźļ▓öņ£äļČäĒżļź╝ ĻĘ╝ņé¼ĒĢśĻĖ░ ņ£äĒĢ┤ ļŗżņ¢æĒĢ£ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│Ćņłśļź╝ ņé¼ņÜ®ĒĢśņŚ¼ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢ£ ļ¬©ļŹĖņØ┤ļ®░, JBļ¬©ļŹĖ Ēö╝ļĪ£ņåÉņāü(DJB)ņØĆ ņŗØ (21)Ļ│╝ Ļ░Öļŗż. ņØ┤ ļ¬©ļŹĖņŚÉ ņé¼ņÜ®ļÉ£ Ļ│äņłśļŖö ņŗØ (22) ~ ņŗØ (31)Ļ│╝ Ļ░Öļŗż.
ņŗØ (21)ņØś c1, c2, c3, ŽāGau ĻĘĖļ”¼Ļ│Ā ŽāRay ļŖö c2, c3, ŽāGau Ļ░ÆņØ┤ ņØīņłśĻ░Ć ļÉśļŖö Ļ▓āņØä Ēö╝ĒĢśĻĖ░ ņ£äĒĢ┤ ņĪ░Ļ▒┤ņŚÉ ļö░ļØ╝ ņŗØ (22) ~ ņŗØ (26) ļśÉļŖö ņŗØ (27) ~ ņŗØ (31)ļĪ£ ņŻ╝ņ¢┤ņ¦äļŗż.
ĻĘĖ ņÖĖņØś Ļ▓ĮņÜ░ņŚÉļŖö
ņŚ¼ĻĖ░ņä£
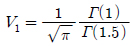
,
CMMR(1) =
╬▒2,
CMMR(2) =
╬▒0.95╬▒1.97,
CMMR(3) =
╬▒0.54╬▒0.93╬▒1.95ņØ┤ļŗż.
ņØ┤ ļ¬©ļŹĖļÅä ņĀĢļ”¼ĒĢśļ®┤, ņŗØ (32)ņÖĆ Ļ░ÖņØ┤ ņāüņłśĒĢŁ
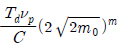
ņŚÉ
fJB(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.
2.3 ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāü
ņ£äņŚÉ ņåīĻ░£ĒĢ£ Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖļōżņØä ņĀĢļ”¼ĒĢ£ ĒśĢĒā£ļź╝ ļ│┤ļ®┤ ļ¬©ļæÉ ĒŖ╣ņĀĢĒĢ£ ĒĢ©ņłśņŚÉ
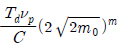
Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż. ļö░ļØ╝ņä£ ņŗØ (10), ņŗØ (17), ņŗØ (20) ĻĘĖļ”¼Ļ│Ā ņŗØ (32)ļĪ£ļČĆĒä░ Ēö╝ļĪ£ņåÉņāüņØä
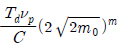
ņ£╝ļĪ£ ļéśļłäļ®┤
fWL(
m,
╬▒2) ,
fDK(
m,
╬▒1,
╬▒2),
fBT(
m,
╬▒1,
╬▒2) ĻĘĖļ”¼Ļ│Ā
fJB(
m,
╬▒0.54,
╬▒0.93,
╬▒0.95,
╬▒1.95,
╬▒2)Ļ░Ć ļÉśĻ│Ā, 2.2ņĀłņŚÉņä£ ļČäņäØĒĢ£ ĻĖ░ņĪ┤ņØś Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖļōżņØĆ
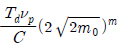
ļź╝ ņĀ£ņÖĖĒĢśļ®┤ S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżļĪ£ ņĪ░ĒĢ®ļÉ£ ļ│Ąņ×ĪĒĢ£ ļŗżĒĢŁņŗØ ļ░Å ĒĢ©ņłśļĪ£ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢ£ Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ņ”ē, Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØĆ ļ│Ąņ×ĪĒĢ£ ļŗżĒĢŁņŗØĻ│╝ ĒĢ©ņłśņØ┤ņ¦Ćļ¦ī ņØ┤ ĒĢ©ņłśļōżņØś ļÅģļ”Įļ│ĆņłśļŖö ļŗ©ņ¦Ć S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżņØ┤ ļÉśļ®░, Ēö╝ļĪ£ņåÉņāüņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ņÜöņåīļŖö S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżļĪ£ ņĀĢĻĘ£ĒÖöņŗ£Ēé¼ ņłś ņ׳ņØīņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļź╝ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØ┤ļØ╝Ļ│Ā ņĀĢņØśĒĢśņśĆņ£╝ļ®░, ņŗØ (33)Ļ│╝ Ļ░ÖņØ┤ ļéśĒāĆļé┤ņŚłļŗż.

ņØ┤ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØĆ S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĖņŚÉ ņé¼ņÜ®ļÉ£ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżņØ┤ Ēö╝ļĪ£ņåÉņāüņŚÉ ņ¢╝ļ¦łļéś ņśüĒ¢źņØä ļ»Ėņ╣śļŖöņ¦Ć ņĢīņĢäļé┤ĻĖ░ ņÜ®ņØ┤ĒĢ£ ĒśĢĒā£ņØ┤ļ®░, ļ╣äņäĀĒśĢ ļ¼ĖņĀ£ņŚÉņä£ļÅä ņĀüĒĢ®ĒĢ£ ĒĢ©ņłśļź╝ ņĀ£Ļ│ĄĒĢ┤ņŻ╝ļŖö ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØĻ│╝ Ļ▓░ĒĢ®ĒĢśņŚ¼ ņé¼ņÜ®ĒĢśļ®┤ ņ×äņØśņØś ĒśĢņāüņØś ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢśņŚ¼ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢĀ ņłś ņ׳Ļ│Ā ņ¢┤ļ¢ĀĒĢ£ ņČöĻ░ĆņĀüņØĖ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśĻ░Ć Ēö╝ļĪ£ņåÉņāüņŚÉ ļ»╝Ļ░ÉĒĢ£ ņśüĒ¢źņØä ņŻ╝ļŖöņ¦Ćļź╝ ņ░ŠņĢäļé╝ ņłś ņ׳ļŗż.
3. Ļ┤æļīĆņŚŁ ņØæļŗĄ ņŖżĒÄÖĒŖĖļ¤╝ ņŗ£ļ«¼ļĀłņØ┤ņģś
3.1 Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝
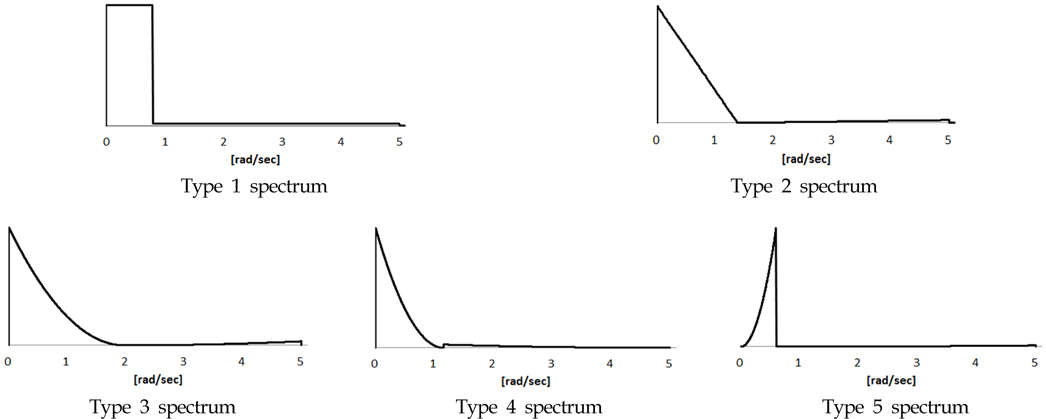
Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņØĆ ļŗżņ¢æĒĢ£ ĒśĢņāüņØä Ļ░Ćņ¦ł ņłś ņ׳ņ£╝ļéś Ļ┤æļīĆņŚŁ ņØæļŗĄ ņŖżĒÄÖĒŖĖļ¤╝ņØś Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ┤ Benasciutti-TovoĻ░Ć ņĀ£ņĢłĒĢ£
Fig. 2ļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż. ņØ┤ļ¤¼ĒĢ£ ņŖżĒÄÖĒŖĖļ¤╝ņØĆ ļ│ĄĒĢ®ņĀüņ£╝ļĪ£ ņ×æņÜ®ĒĢśļŖö ļÅÖņĀüĒĢśņżæņØä ņØ┤ņāüĒÖöĒĢ£ Ļ▓āņØ┤ļ®░, ņåīĻ░£ļÉ£ Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖļōżļÅä ņØ┤ļ¤¼ĒĢ£ ņóģļźśņØś Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņØä ņāØņä▒ĒĢśņŚ¼ ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ņØ┤ļ¤¼ĒĢ£ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ĒīīļØ╝ļ®öĒä░
S1,
S2,
Žē1,
Žē2,
Žē3ļź╝ ņĪ░ņĀĢĒĢśņŚ¼ Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņØä ņāØņä▒ĒĢśņŚ¼ ņ¢┤ļ¢ĀĒĢ£ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśĻ░Ć Ēö╝ļĪ£ņåÉņāüņŚÉ ļ»╝Ļ░ÉĒĢ£ņ¦Ćļź╝ Ļ▓ĆĒåĀĒĢ┤ ļ│┤Ļ│Āņ×É ĒĢ£ļŗż.
Fig.┬Ā2
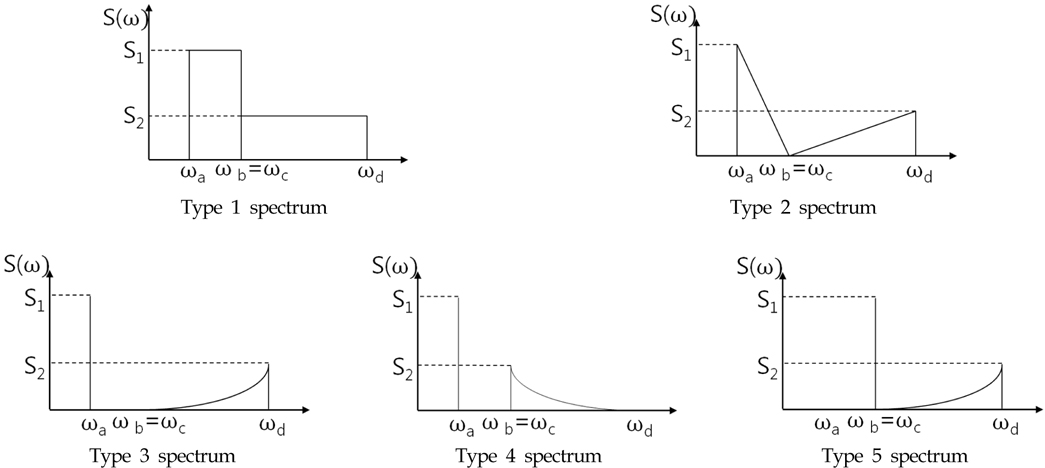
Fig. 2ņØś 5Ļ░Ćņ¦Ć ņóģļźśņØś Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£
Table 1Ļ│╝ Ļ░ÖņØ┤
S1,
S2,
Žē1,
Žē2,
Žē3ļź╝ ņĪ░ņĀĢĒĢśņŚ¼ ņ┤Ø 540Ļ░Ćņ¦Ć ņŖżĒÄÖĒŖĖļ¤╝ņØä ņāØņä▒ĒĢśņśĆļŗż.
Table┬Ā1
Range of spectrum parameters
3.2 ņŗ£Ļ░äņśüņŚŁ ņŗ£ļ«¼ļĀłņØ┤ņģś
ņŗ£Ļ░äņśüņŚŁ ņŗ£ļ«¼ļĀłņØ┤ņģśņØĆ
Park(2011)ņØ┤ ņĀ£ņĢłĒĢ£ ļ░®ļ▓Ģņ£╝ļĪ£
Fig. 3Ļ│╝ Ļ░ÖņØ┤ ĒĢ£ Ļ░£ņØś ļĖöļĪØņØĆ 60ņŗ£Ļ░äņ£╝ļĪ£ ņĀäĻ░£ĒĢśņśĆņ£╝ļ®░, 10Ļ░£ņØś ļĖöļĪØņØä ņłśĒ¢ēĒĢśņśĆņ£╝ļ»ĆļĪ£ ĒĢ£ Ļ░£ņØś ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢśņŚ¼ 600ņŗ£Ļ░äņØś ņŗ£Ļ│äņŚ┤ ļŹ░ņØ┤Ēä░ļź╝ ņ¢╗ņŚłļŗż.
Fig.┬Ā3

ĒĢ£ Ļ░£ņØś ļĖöļĪØņŚÉ ļīĆĒĢśņŚ¼ ļĀłņØĖĒöīļĪ£ņÜ░ ņ¦æĻ│äļ▓ĢņØä ņé¼ņÜ®ĒĢśņŚ¼ ņØæļĀźļ▓öņ£ä ļČäĒżļź╝ ĻĄ¼ņśĆĻ│Ā, 10Ļ░£ ļĖöļĪØņŚÉņä£ ĻĄ¼ĒĢ£ ņØæļĀźļ▓öņ£ä ļČäĒżļź╝ ĒĢ®ĒĢśņŚ¼ ņĄ£ņóģ ņØæļĀźļ▓öņ£äļČäĒżļź╝ ĻĄ¼ĒĢśņśĆļŗż. ņØ┤ ļĢī ņŖżĒÄÖĒŖĖļ¤╝ņ£╝ļĪ£ļČĆĒä░ ņŗ£Ļ░äņśüņŚŁņ£╝ļĪ£ ĒÖĢņןĒĢśĻĖ░ ņ£äĒĢ┤ ņŗ£Ļ░äĻ░äĻ▓®ņØĆ 0.1ņ┤łļź╝ ņé¼ņÜ®ĒĢśņśĆĻ│Ā ļ¼┤ņ×æņ£ä ņŻ╝Ēīīņłś Ļ░äĻ▓®ņØĆ 20,000Ļ░£ļź╝ ņāØņä▒ĒĢśņśĆļŗż.
4. ņØĖĻ│Ą ņŗĀĻ▓Įļ¦Ø ņØ┤ļĪĀ
ņØĖĻ│Ą ņŗĀĻ▓Įļ¦ØņØĆ ņ×ģļĀźĻ░Æ(Input value)Ļ│╝ ļ¬®Ēæ£ ņČ£ļĀźĻ░Æ(Target output value) Ļ░äņØś Ļ┤ĆĻ│äļź╝ ņČöļĪĀĒĢśņŚ¼ ņØ┤ļōż ņé¼ņØ┤ņŚÉ ĒśĢņä▒ļÉśļŖö ļ»Ėņ¦ĆņØś ņŗ£ņŖżĒģ£ņØä ņŗØļ│äĒĢśļŖö Ļ░ĢļĀźĒĢ£ ļ░®ļ▓ĢņØ┤ļŗż. ņØ┤ļŖö
Fig. 4ņÖĆ Ļ░ÖņØ┤ ņé¼ļ×īņØś ļćīņŗĀĻ▓Įļ¦ØņØä ļŗ©ņł£ĒÖöĒĢ£ ĒśĢĒā£ļĪ£ņä£ ņŚ¼ļ¤¼ Ļ░Ćņ¦Ć ņ×ģļĀź ļŹ░ņØ┤Ēä░ļź╝ ņØ┤ņÖĆ ņŚ░Ļ▓░ļÉ£ ļē┤ļ¤░ņØä ĒåĄĒĢśņŚ¼ Ļ░Ćņżæņ╣śļź╝ Ļ│▒ĒĢśĻ│Ā ĒĢ®ņ│Éņä£ ņ▓śļ”¼ĒĢ£ Ēøä, ĻĘĖ Ļ▓░Ļ│╝ Ļ░ÆņØä ĒÖ£ņä▒ĒÖö ĒĢ©ņłś(Activation function)ņØä Ļ▒░ņ│É Ļ░äļŗ©ĒĢ£ Ļ▓ĮņÜ░ ĒĢ£Ļ│äĻ░ÆņØä ļäśņ£╝ļ®┤ 1ņØä ĻĘĖļĀćņ¦Ć ņĢŖņ£╝ļ®┤ ŌĆō1ņØä ņČ£ļĀźĒĢśņŚ¼ ļŗżņØī ļģĖļō£ņŚÉ Ļ▓░Ļ│╝ļź╝ ņĀäļŗ¼ĒĢśļŖö ļ░®ņŗØņØ┤ļŗż. ņØ┤ļ¤¼ĒĢ£ ļ░®ņŗØņØä ĒåĄĒĢśņŚ¼ ļ»Ėņ¦ĆņØś ņŗ£ņŖżĒģ£ņØ┤ ļ╣äņäĀĒśĢņä▒ņØä ĒżĒĢ©ĒĢśņŚ¼ļÅä ņČöņĀĢņØ┤ Ļ░ĆļŖźĒĢśĻ▓ī ļÉ£ļŗż.
Fig.┬Ā4
Multi-layer perceptron neural network
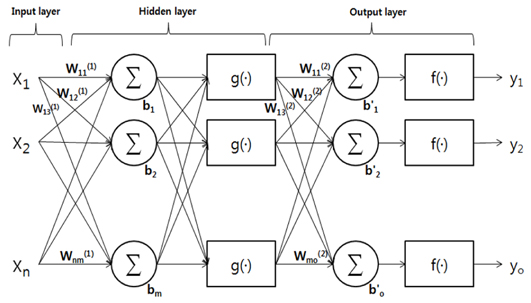
ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņŚÉņä£ Ļ░Ćņן ļ¦ÄņØ┤ ņé¼ņÜ®ļÉśļŖö ļ░®ņŗØņØĆ ļŗżņĖĄ ĒŹ╝ņģēĒŖĖļĪĀ ņŗĀĻ▓Įļ¦ØņØ┤Ļ│Ā ņØ┤ļŖö
Fig. 4ņÖĆ Ļ░ÖņØ┤ ņ×ģļĀźņĖĄ(Input layer)Ļ│╝ ņČ£ļĀźņĖĄ(Output layer) ņé¼ņØ┤ņŚÉ ņØĆļŗēņĖĄ(Hidden layer)ņØä ļæÉņ¢┤ņä£ ņŗ£ņŖżĒģ£ņØś ņŗØļ│äņŚÉ ņ£ĀņŚ░ņä▒ņØä ļČĆĻ│╝ĒĢ£ Ļ▓āņØ┤ļ®░, ņØ┤ļ¤¼ĒĢ£ Ļ│╝ņĀĢņØä ņŗØņ£╝ļĪ£ ļéśĒāĆļé┤ļ®┤ ņŗØ (34)ņÖĆ Ļ░ÖņØ┤ ĻĘ╝ņé¼ļ░®ņĀĢņŗØņØä ņ¢╗Ļ▓ī ļÉ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉ ņé¼ņÜ®ļÉ£ ņŗØ(34)ņØś ņ×ģļĀźņĖĄņØś ļ│Ćņłś xi ļŖö ņŗØ(33)Ļ│╝ Ļ░ÖņØ┤ m, ai Ļ│╝ ļÉśĻ│Ā, ņČ£ļĀźņĖĄņØś ykļŖö ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØ┤ ļÉ£ļŗż.
Ļ░ü ļē┤ļ¤░ņØĆ
Fig. 4ņÖĆ Ļ░ÖņØ┤ Ļ░Ćņżæņ╣śļź╝ Ļ░Ćņ¦ĆĻ│Ā ņŚ░Ļ▓░ņØ┤ ļÉśņ¢┤ ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ ļ░śļ│ĄņĀüņØĖ ņĪ░ņĀĢĒĢÖņŖĄņØä ĒåĄĒĢśņŚ¼ ņŗØ(34)ņØś Ļ▓░Ļ│╝Ļ░ÆĻ│╝
Fig. 3ņ£╝ļĪ£ļČĆĒä░ ņ¢╗ņØĆ ļ¬®Ēæ£ ņČ£ļĀźĻ░ÆņØś ņśżņ░©Ļ░Ć ņĄ£ņåīĒÖöļÉśļÅäļĪØ Ļ░Ćņżæņ╣śļōżņØ┤ ņĪ░ņĀĢļÉśļ®░, ĻĘĖ ļīĆĒæ£ņĀüņØĖ ļ░®ļ▓Ģņ£╝ļĪ£ļŖö ņŚŁņĀäĒīī(Back propagation)ļ░®ļ▓ĢņØ┤ ņ׳ļŗż.
5. Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝Ļ│╝ Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖ Ļ▓ĆĒåĀ
ņ£äņØś 2.2ņĀłņŚÉņä£ ņåīĻ░£ĒĢ£ ļ¬©ļŹĖļōż ņżæņŚÉņä£ JBļ¬©ļŹĖņØä ņĀ£ņÖĖĒĢ£ Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖļōżņØĆ Ēö╝ļĪ£ņåÉņāüņØś ĒŖ╣ņ¦ĢņØä ļéśĒāĆļé┤ļŖö ņØĖņ×ÉļōżņØ┤
m,
╬▒2 ļśÉļŖö
m,
╬▒1,
╬▒2ļØ╝Ļ│Ā ņĀ£ņĢłļÉśņ¢┤ņĀĖ ņś© Ļ▓āņØä ņĢī ņłś ņ׳ļŗż.
Fig. 2ņØś 5Ļ░Ćņ¦Ć Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢśņŚ¼
S1,
S2,
Žē1,
Žē2,
Žē3ļź╝ ņĀüņĀłĒ׳ ņĪ░ņĀĢĒĢśļ®┤
Fig. 5ņÖĆ Ļ░ÖņØ┤ ņä£ļĪ£ ļŗżļźĖ ĒśĢņāüņØ┤ņ¦Ćļ¦ī ļÅÖņØ╝ĒĢ£
╬▒1Ļ│╝
╬▒2ļź╝ Ļ░¢ļÅäļĪØ ĒĢĀ ņłś ņ׳ļŗż. ļ¦īņĢĮ Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØś
m,
╬▒1,
╬▒2Ļ░Ć Ēö╝ļĪ£ņåÉņāüņØä Ēæ£ĒśäĒĢśļŖö ņ£ĀņØ╝ĒĢ£ ņØĖņ×ÉļōżņØ┤ļØ╝ļ®┤,
Fig. 5ņØś ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļÅÖņØ╝ĒĢ£ S-NĻ│ĪņäĀĻ│╝
Fig. 3ņØś ļĀłņØĖĒöīļĪ£ņÜ░ ņ¦æĻ│äļ▓ĢņØä ņĀüņÜ®ĒĢĀ Ļ▓ĮņÜ░ņŚÉ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØĆ ļ¬©ļæÉ ļÅÖņØ╝ĒĢ£ Ļ░ÆņØä ļéśĒāĆļé┤ņ¢┤ņĢ╝ ĒĢ£ļŗż. ĒĢśņ¦Ćļ¦ī
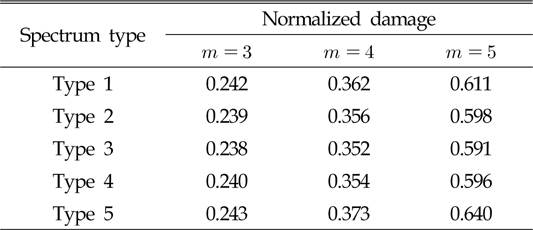
Table 2ņŚÉņä£ ļ│┤ņØ┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤
Fig. 5ņØś ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ£ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØĆ ļ¬©ļæÉ ņāüņØ┤ĒĢ©ņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļŖö JBļ¬©ļŹĖņØä ņĀ£ņÖĖĒĢ£ ĻĖ░ņĪ┤ņØś Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņŚÉ ņé¼ņÜ®ļÉ£
m,
╬▒2 ļśÉļŖö
m,
╬▒1,
╬▒2Ļ░Ć Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśĻĖ░ļŖö ĻĘĖ ņØĖņ×ÉņØś ņłśĻ░Ć ļČĆņĪ▒ĒĢ©ņØä ņĢī ņłś ņ׳ņ£╝ļ®░, ņČöĻ░ĆņĀüņØĖ ņØĖņ×ÉĻ░Ć ĒĢäņÜöĒĢ©ņØä ņĢī ņłś ņ׳ļŗż. ļśÉĒĢ£
m,
╬▒1,
╬▒2ļź╝ ņ×ģļĀźņĖĄņ£╝ļĪ£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ĻĄ¼ņä▒ĒĢśņŚ¼ļÅä ņŗØ (34)ņØś ĒĢ©ņłśņĪ░Ļ▒┤ņØä ļ¦īņĪ▒ĒĢĀ ņłś ņŚåņ¢┤ ņØ╝Ļ┤ĆņĀüņØĖ ņČ£ļĀźņØä ņ¢╗ņØä ņłś ņŚåņØīņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā5
Wide band spectrum with ╬▒1 = 0.6 and ╬▒2 = 0.3
Table┬Ā2
Normalized fatigue damage for each type with ╬▒1 = 0.6 and ╬▒2 = 0.3
ņØ┤ļź╝ ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢ┤ņä£ Ēö╝ļĪ£ņåÉņāüņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ņČöĻ░ĆņĀüņØĖ ņØĖņ×Éļź╝ ļ»╝Ļ░ÉļÅä ĒĢ┤ņäØņØä ĒåĄĒĢśņŚ¼ Ļ▓ĆĒåĀĒĢśĻ│Ā, ņØ┤ļź╝ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØś ņ×ģļĀźņĖĄņŚÉ ļ░śņśüĒĢśļŖö Ļ▓āņØ┤ ļ░öļ×īņ¦üĒĢśļŗż. ņŗżņĀ£ ĒĢ┤ņ¢æĒöīļ×£ĒŖĖ Ļ│Ąņé¼ņÖĆ Ļ░ÖņØ┤ ņŚ¼ļ¤¼ Ļ░£ņØś ņŚöņ¦Ćļŗłņ¢┤ļ¦ü ņŚģņ▓┤ļĪ£ļČĆĒä░ ļÅÖĒĢśņżæņØä ļ░øņĢäņä£ ņØ┤ļź╝ ĒåĄĒĢ®ĒĢśņŚ¼ Ēö╝ļĪ£ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśļŖö Ļ▓ĮņÜ░ņŚÉļŖö ņØæļŗĄ ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĀ£Ļ│ĄĒĢśņ¦Ć ņĢŖĻ│Ā ņŖżĒÄÖĒŖĖļ¤┤ ļ¬©ļ®śĒŖĖļź╝ ņĀ£Ļ│ĄĒĢśļŖö Ļ▓ĮņÜ░Ļ░Ć ļ¦ÄĻĖ░ ļĢīļ¼ĖņŚÉ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśļŖöļŹ░ JBļ¬©ļŹĖņ▓śļ¤╝ ļ│Ąņ×ĪĒĢ£ ņØĖņ×Éļéś ļ¦ÄņØĆ ņłśņØś ņØĖņ×Éļź╝ Ļ│ĀļĀżĒĢśļŖö Ļ▓āņØĆ ļ╣äĒśäņŗżņĀüņØ┤ļŗż. ļŗ©ņØ╝ ĒöäļĪ£ĻĘĖļש ļé┤ņŚÉņä£ ņØæļŗĄ ņŖżĒÄÖĒŖĖļ¤╝ņ£╝ļĪ£ļČĆĒä░ Ēö╝ļĪ£ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśļŖö Ļ▓ĮņÜ░ļŖö ņāüĻ┤ĆņØ┤ ņŚåņ¦Ćļ¦ī, ĻĘĖļĀćņ¦Ć ņĢŖņØĆ Ļ▓ĮņÜ░ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņĄ£ņåīĒĢ£ņØś ņØĖņ×ÉļĪ£ Ēö╝ļĪ£ņåÉņāüņØä ļŗżļŻ©ļŖö Ļ▓āņØ┤ ļ│┤ļŗż ĒśäņŗżņĀüņØ╝ Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż. ļö░ļØ╝ņä£ ņČöĻ░ĆņĀüņØĖ ņØĖņ×Éļź╝ Ļ▓░ņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņłśļ¦ÄņØĆ Ļ▓ĮņÜ░ļź╝ Ļ▓ĆĒåĀĒĢ┤ņĢ╝ ĒĢśļéś, ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö
╬▒0.75ņÖĆ
╬▒1.5ņŚÉ ļīĆĒĢ┤ņä£ ļ»╝Ļ░ÉļÅä ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśļĀżĻ│Ā ĒĢ£ļŗż. ņØ┤ļŖö
╬▒0.75Ļ░Ć Wirsching-Light ļ¬©ļŹĖņØś ļ│┤ņĀĢĻ│äņłśņØĖ
ŽüWL ņÖĆ Ļ░ÖņØ┤ ņé¼ņÜ®ļÉśļŖö ļ¬©ļŹĖņØ┤ ņ׳ĻĖ░ ļĢīļ¼ĖņØ┤ļ®░(
Benasciutti, 2004),
╬▒1.5ļŖö
╬▒1ņÖĆ
╬▒2ņØś Ļ░ĆņÜ┤ļŹ░ Ļ░Æņ£╝ļĪ£ Ēö╝ļĪ£ņåÉņāüņŚÉ ņĀüņĀłĒĢ£ ļ»╝Ļ░ÉļÅäļź╝ ļ│┤ņØ╝ Ļ▓āņ£╝ļĪ£ ņśłņĖĪļÉśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
6. Ļ▓░Ļ│╝ ļ░Å ļČäņäØ
ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØĆ
╬▒1 ,
╬▒2ņÖĖņŚÉ ņČöĻ░ĆņĀüņ£╝ļĪ£
╬▒0.75ņÖĆ
╬▒1.5ņØĖņ×Éļź╝ ņ×ģļĀźĻ░Æņ£╝ļĪ£ ņé¼ņÜ®ĒĢśņśĆĻ│Ā, ĒĢ£ Ļ░£ņØś ņØĆļŗēņĖĄņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņśĆļŗż. ĒÖ£ņä▒ĒÖö ĒĢ©ņłś(Activation function)ļŖö ņØĆļŗēņĖĄņŚÉņä£ ņīŹĻ│ĪĒāäņĀĀĒŖĖĒĢ©ņłś(Hyperbolic tangent function), ņČ£ļĀźņĖĄņŚÉņä£ ņäĀĒśĢĒĢ©ņłś(Linear function)ļź╝ ņĀüņÜ®ĒĢśņśĆļŗż. ņØĆļŗēņĖĄ ņŗĀĻ▓ĮĻ░£ņłśļŖö ļæÉ ņóģļźśļĪ£ Ļ░üĻ░ü 10Ļ░£ņÖĆ 30Ļ░£ļź╝ ņĀüņÜ®ĒĢśņŚ¼ ņ┤Ø 8Ļ░£ņØś ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä
Table 3Ļ│╝ Ļ░ÖņØ┤ ĻĄ¼ņä▒ĒĢśņśĆņ£╝ļ®░,
Table 1 ņŚÉņä£ ņāØņä▒ļÉ£ ņ┤Ø 540Ļ░£ ļŹ░ņØ┤Ēä░ņŚÉņä£ ļ¼┤ņ×æņ£äļĪ£ 70%ļŖö ĒĢÖņŖĄņØä ņ£äĒĢ£ ĒĢÖņŖĄ ņäĖĒŖĖ(Training data set), 15%ļŖö ĒĢÖņŖĄņżæņŚÉ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØś Ļ│╝ņĀüĒĢ®(Overfitting)ņØä Ļ▓ĆĒåĀĒĢśļŖö Ļ▓ĆĒåĀ ņäĖĒŖĖ(Validation data set) ĻĘĖļ”¼Ļ│Ā 15%ļŖö ņÖäņä▒ļÉ£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ĒģīņŖżĒŖĖ ĒĢśļŖö ĒģīņŖżĒŖĖ ņģŗĒŖĖ(Test data)ļĪ£ ĻĄ¼ņä▒ĒĢśņśĆļŗż. ņØ┤ļ¤¼ĒĢ£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØ┤ ĒĢÖņŖĄļÉśņ¦Ć ņĢŖņØĆ Ļ▓ĮņÜ░ņŚÉ ļīĆĒĢśņŚ¼ ņ¢┤ļ¢ĀĒĢ£ Ļ▓░Ļ│╝ļź╝ ņŻ╝ļŖöņ¦Ć Ļ▓ĆĒåĀĒĢśĻĖ░ ņ£äĒĢśņŚ¼
Fig. 2ņØś 5Ļ░Ćņ¦Ć ņóģļźśņØś Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£
Table 4ņÖĆ Ļ░ÖņØ┤
S1,
S2,
Žē1,
Žē2,
Žē3 ļź╝ ņĪ░ņĀĢĒĢśņŚ¼ ņ┤Ø 10Ļ░£ņØś ņŖżĒÄÖĒŖĖļ¤╝ņØä ņāØņä▒ĒĢśņśĆļŗż. Ļ│äņé░ņØś ņĀĢĒÖĢļÅäļŖö ņØĖĻ│ĄņŗĀĻ▓Įļ¦Øņ£╝ļĪ£ ĻĄ¼ĒĢ£ Ēö╝ļĪ£ņåÉņāüĻ│╝ ļĀłņØĖĒöīļĪ£ņÜ░ ņ¦æĻ│äļ▓Ģņ£╝ļĪ£ ĻĄ¼ĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ļ╣äĻĄÉĒĢśņŚ¼ ĻĄ¼ĒĢśņśĆņ£╝ļ®░, ņØ┤ļź╝ ņ£äĒĢ┤ ņśżņ░©ņ£©(EI, Error index)ņØä ņŗØ(35)ņÖĆ Ļ░ÖņØ┤ ņé¼ņÜ®ĒĢśņśĆļŗż.
Table┬Ā3
Artificial neural network formation

Table┬Ā4
Artificial neural network test cases

ņŚ¼ĻĖ░ņä£, DANN ņÖĆ DRFC ļŖö ņØĖĻ│ĄņŗĀĻ▓Įļ¦Øņ£╝ļĪ£ļČĆĒä░ ņČöņĀĢĒĢ£ Ēö╝ļĪ£ņåÉņāüĻ│╝ ļĀłņØĖĒöīļĪ£ņÜ░ ņ¦æĻ│äļ▓Ģņ£╝ļĪ£ ĻĄ¼ĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ļéśĒāĆļéĖļŗż.
Table 3ņ£╝ļĪ£ ĻĄ¼ņä▒ļÉ£ 8Ļ░£ņØś ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņŚÉ ļīĆĒĢśņŚ¼
Table 1Ļ│╝
Table 4ņŚÉ ļīĆĒĢ£ ņśżņ░©ņ£©ņØĆ
Table 5ņÖĆ Ļ░Öļŗż.
╬▒1 ,
╬▒2 ,
m ņ£╝ļĪ£ ĻĄ¼ņä▒ļÉ£ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØĆ ĒĢ©ņłśņĪ░Ļ▒┤ņØ┤ ļ¦īņĪ▒ļÉśņ¦Ć ņĢŖĻĖ░ ļĢīļ¼ĖņŚÉ ņĀäļ░śņĀüņ£╝ļĪ£ ļåÆņØĆ ņśżņ░©ņ£©ņØä ļ│┤ņØ┤Ļ│Ā ņ׳ļŗż. ļæÉ Ļ░£ņØś ņČöĻ░ĆņĀüņØĖ ņØĖņłśļź╝ Ļ░Ćņ¦ä N07515-H10ņÖĆ N07515-H30ļŖö Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£ļŖö ļ¦żņÜ░ ļé«ņØĆ ņśżņ░©ņ£©ņØä Ļ░Ćņ¦ĆĻ│Ā ņ׳ņ¦Ćļ¦ī ĒĢÖņŖĄļÉśņ¦Ć ņĢŖņØĆ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£ļŖö ļåÆņØĆ ņśżņ░©ņ£©ņØä ļ│┤ņśĆļŗż. ņĀäļ░śņĀüņ£╝ļĪ£ ņØĆļŗēņĖĄņØś ņŗĀĻ▓Į Ļ░£ņłśĻ░Ć ļ¦ÄņØĆ H30ņØś Ļ▓ĮņÜ░, ĒĢÖņŖĄļÉ£ Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£ļŖö ņāüļīĆņĀüņ£╝ļĪ£ ļé«ņØĆ ņśżņ░©ņ£©ņØä ļ│┤ņØ┤ļéś ĒĢÖņŖĄļÉśņ¦Ć ņĢŖņØĆ Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£ļŖö ļåÆņØĆ ņśżņ░©ņ£©ņØä ļ│┤ņØ┤Ļ│Ā ņ׳ļŗż. ņØ┤ļŖö ļåÆņØĆ ņ░©ņłśņØś H30 ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØ┤ ĒĢÖņŖĄļÉśņ¦Ć ņĢŖņØĆ Ļ▓ĮņÜ░ņŚÉ ļīĆĒĢ┤ņä£ ļĀłņØĖĒöīļĪ£ņÜ░ ņ¦æĻ│äļ▓Ģņ£╝ļĪ£ ĻĄ¼ĒĢ£ Ēö╝ļĪ£ņåÉņāüĻ░Æ ņŻ╝ļ│ĆņŚÉ ļåÆņØĆ ļÅÖņÜö(Oscillation)ņØ┤ ļ░£ņāØĒĢśņŚ¼ ļ¦żņÜ░ ņ░©ņØ┤Ļ░Ć ļéśļŖö Ļ▓░Ļ│╝ļź╝ ņĀ£Ļ│ĄĒĢ£ Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż. ņØ┤ļŖö ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØś ĒŖ╣ņä▒ņ£╝ļĪ£ņä£ H30ņØś Ļ▓░Ļ│╝ļĪ£ Ēö╝ļĪ£ņåÉņāüņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢ£ ņĀüĒĢ®ĒĢ£ ņØĖņ×Éļź╝ ĒīÉļŗ©ĒĢśĻĖ░ļŖö ņ¢┤ļĀĄļŗż. ļö░ļØ╝ņä£
Fig. 2ņÖĆ Ļ░ÖņØĆ Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£ ņśżņ░©ņ£©ņØ┤ Ļ░Ćņן ļé«ņØĆ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØĆ N15-H10ņØ┤ļ®░,
╬▒1.5Ļ░Ć ņČöĻ░ĆņĀüņØĖ ņØĖņ×ÉļĪ£ ņé¼ņÜ®ļÉĀ ņłś ņ׳ņØīņØä ņĢī ņłś ņ׳ļŗż.
Table┬Ā5
Error Index for wide band spectrum and test cases

ņØĖĻ│ĄņŗĀĻ▓Įļ¦Ø N15-H10ņŚÉ ļīĆĒĢ£
Table 1Ļ│╝
Table 4ņØś Ēö╝ļĪ£ņåÉņāüļ╣ä ļČäĒżļź╝ Van Marcke ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļĪ£ ļéśĒāĆļé┤ļ®┤ Ļ░üĻ░ü
Fig. 6Ļ│╝
Fig. 7Ļ│╝ Ļ░Öļŗż.
Fig. 7ņŚÉņä£ ĒĢ£ Ļ░£ņØś Ļ▓░Ļ│╝ Ļ░ÆņØ┤ ņ×æņØĆ Ēö╝ļĪ£ņåÉņāüņØä ņČöņĀĢĒĢśĻ│Ā ņ׳ņ£╝ļéś, ņØ┤ļŖö ņóĆ ļŹö ļ¦ÄņØĆ ņŖżĒÄÖĒŖĖļ¤╝ņØä ĒĢÖņŖĄĒĢ©ņ£╝ļĪ£ ņØĖĒĢ┤ Ļ░£ņäĀļÉĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.
Fig.┬Ā6
Fatigue damage ratio with N15-H10 for wide band spectrum
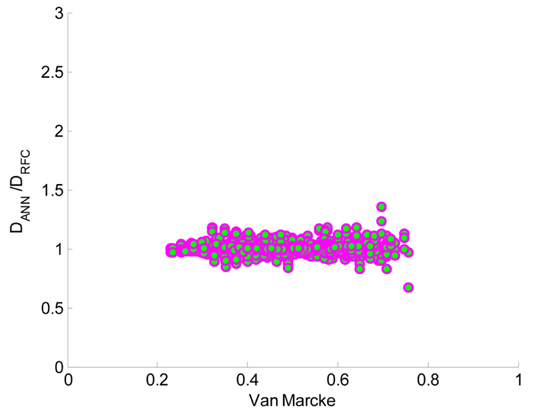
Fig.┬Ā7
Fatigue damage ratio with N15-H10 for test cases
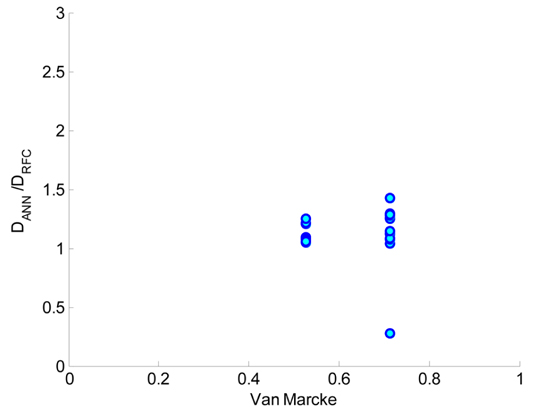
Fig. 7ņŚÉņä£ Ēö╝ļĪ£ņåÉņāüļ╣äĻ░Ć ļæÉ Ļ░£ņØś Van Marcke ļ░┤ļō£ĒÅŁņŚÉ ļīĆĒĢ┤ņä£ ļéśņśżļŖö Ļ▓āņØĆ Van Marcke ļ░┤ļō£ĒÅŁņØĆ
╬▒1ņŚÉ ļīĆĒĢ£ ĒĢ©ņłśņØ┤Ļ│Ā
Table 4ņØś Ļ▓ĮņÜ░
╬▒1ņØ┤ 0.7Ļ│╝ 0.85ņØĖ Ļ▓ĮņÜ░ļ¦ī ņ׳ĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
7. Ļ▓░ ļĪĀ
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ×äņØśņØś ĒśĢņāüņØä Ļ░Ćņ¦ĆļŖö Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢ£ ĻĖ░ņ┤łņŚ░ĻĄ¼ļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØä ņĀĢņØśĒĢśņśĆņ£╝ļ®░, ņØ┤ļĪ£ļČĆĒä░ ļīĆļČĆļČäņØś ĻĖ░ņĪ┤ Ēö╝ļĪ£ņåÉņāü ļ¬©ļŹĖņØ┤ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņŚÉ ļīĆĒĢśņŚ¼ m, ╬▒2 ļśÉļŖö m, ╬▒1, ╬▒2ņØś ĒĢ©ņłśļĪ£ ļéśĒāĆļāäņØä ņĢī ņłś ņ׳ņŚłļŗż. ļŗżņ¢æĒĢ£ ĒśĢņāüņØś Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢśņŚ¼ ņŗ£Ļ░äņśüņŚŁņŚÉņä£ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņłśĒ¢ēĒĢśņśĆĻ│Ā ļĀłņØĖĒöīļĪ£ņÜ░ ņ¦æĻ│äļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņĀĢĒÖĢĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ĻĄ¼ĒĢśņśĆļŗż. ņØ┤ļĪ£ļČĆĒä░ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüĻ░ÆļōżņØ┤ ļÅÖņØ╝ĒĢ£ S-NĻ│ĪņäĀĻ│╝ ╬▒1Ļ│╝ ╬▒2ņŚÉ ļīĆĒĢśņŚ¼ ņä£ļĪ£ ļŗżļźĖ Ēö╝ļĪ£ņåÉņāüņØä Ļ░¢ļŖö Ļ▓āņØä ņĢī ņłś ņ׳ņŚłņ£╝ļ®░, ņČöĻ░ĆņĀüņØĖ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśĻ░Ć ĒĢäņÜöĒĢ©ņØä ņĢī ņłś ņ׳ņŚłļŗż. ņČöĻ░ĆņĀüņØĖ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļĪ£ ╬▒0.75ņÖĆ ╬▒1.5ļź╝ ļÅäņ×ģĒĢśņśĆņ£╝ļ®░, ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ņé¼ņÜ®ĒĢśņŚ¼ ļ»╝Ļ░ÉļÅä ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż. ņØ┤ļĪ£ļČĆĒä░ ļŗżņØīņØś Ļ▓░ļĪĀņØä ņ¢╗ņØä ņłś ņ׳ļŗż.
(1) ╬▒1.5Ļ░Ć ņ×äņØśņØś Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņØś ĒśĢņāüņŚÉ ļīĆĒĢ£ Ēö╝ļĪ£ņåÉņāüņØä ņČöņĀĢĒĢśļŖöļŹ░ ņśüĒ¢źņØä ļ¦ÄņØ┤ ļ»Ėņ╣śļŖö ņŻ╝ņÜöņØĖņ×ÉņØ┤ļŗż.
(2) ļ¦ÄņØĆ ņØĆļŗēņĖĄ ņŗĀĻ▓Į Ļ░£ņłśļŖö ĒĢÖņŖĄļÉśņ¦Ć ņĢŖņØĆ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśļŖöļŹ░ Ļ│╝ļÅäĒĢ£ ļ│┤Ļ░äĻ░ÆņØä ņé¼ņÜ®ĒĢśņŚ¼ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢśļŖöļŹ░ ņĢģņśüĒ¢źņØä ļ»Ėņ╣Ā ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż.
ņØ┤ļ¤¼ĒĢ£ ņŚ░ĻĄ¼ļŖö ņóĆ ļŹö ļŗżņ¢æĒĢ£ Ļ┤æļīĆņŚŁ ņŖżĒÄÖĒŖĖļ¤╝ņØä ĒĢÖņŖĄĒĢśļ®┤ ņŗĀļó░ņä▒ ņ׳ļŖö ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ĻĄ¼ņä▒ĒĢĀ ņłś ņ׳ņØä ļ┐Éļ¦ī ņĢäļŗłļØ╝ ņØ┤ļ┤ēĒśĢ ļśÉļŖö ņé╝ļ┤ēĒśĢ ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ļīĆĒĢ┤ņä£ļÅä ĒśĢņāüņØä Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖĻ│Ā Ēö╝ļĪ£ņłśļ¬ģņØä ņśłņĖĪĒĢśļŖö Ļ▓āņŚÉ ĒÖ£ņÜ®ļÉĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż. Ē¢źĒøä ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ēö╝ļĪ£ņåÉņāüņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ņØĖņ×Éļź╝ ņ▓┤Ļ│äņĀüņ£╝ļĪ£ ļČäņäØĒĢśļ®┤, ņĀĢļÅä ļåÆņØĆ Ēö╝ļĪ£ņåÉņāü ļ¬©ļŹĖ Ļ░£ļ░£ĒĢśļŖöļŹ░ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.






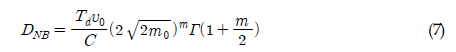
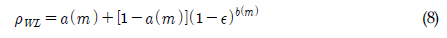
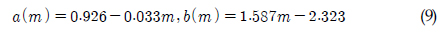
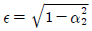 ņØ┤ļŗż.
ņØ┤ļŗż.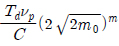 ņŚÉ S-NņäĀļÅäņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä ĒĢ©ņłś fWL(ŌĆó)ņØ┤ Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.
ņŚÉ S-NņäĀļÅäņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä ĒĢ©ņłś fWL(ŌĆó)ņØ┤ Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.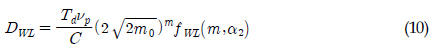
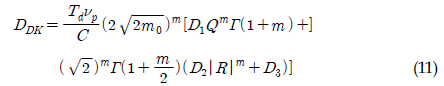



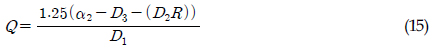

 ņØ┤ļŗż.
ņØ┤ļŗż.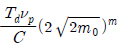 ņŚÉ fDK(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£Ļ░Ć ļÉ£ļŗż.
ņŚÉ fDK(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£Ļ░Ć ļÉ£ļŗż.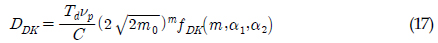

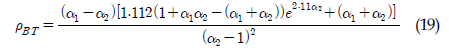
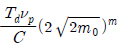 ņŚÉ fBT(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.
ņŚÉ fBT(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.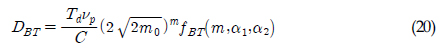
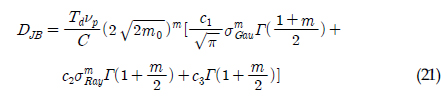
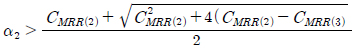 ļśÉļŖö
ļśÉļŖö 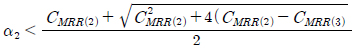 ĻĘĖļ”¼Ļ│Ā
ĻĘĖļ”¼Ļ│Ā  ņØ┤ļ®┤,
ņØ┤ļ®┤,

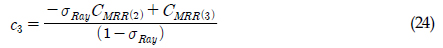







 , CMMR(1) = ╬▒2, CMMR(2) = ╬▒0.95╬▒1.97, CMMR(3) = ╬▒0.54╬▒0.93╬▒1.95ņØ┤ļŗż.
, CMMR(1) = ╬▒2, CMMR(2) = ╬▒0.95╬▒1.97, CMMR(3) = ╬▒0.54╬▒0.93╬▒1.95ņØ┤ļŗż.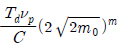 ņŚÉ fJB(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.
ņŚÉ fJB(ŌĆó)Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż.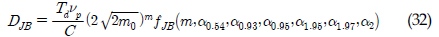
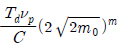 Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż. ļö░ļØ╝ņä£ ņŗØ (10), ņŗØ (17), ņŗØ (20) ĻĘĖļ”¼Ļ│Ā ņŗØ (32)ļĪ£ļČĆĒä░ Ēö╝ļĪ£ņåÉņāüņØä
Ļ░Ć Ļ│▒ĒĢ┤ņ¦ä ĒśĢĒā£ņØ┤ļŗż. ļö░ļØ╝ņä£ ņŗØ (10), ņŗØ (17), ņŗØ (20) ĻĘĖļ”¼Ļ│Ā ņŗØ (32)ļĪ£ļČĆĒä░ Ēö╝ļĪ£ņåÉņāüņØä 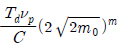 ņ£╝ļĪ£ ļéśļłäļ®┤ fWL(m, ╬▒2) , fDK(m,╬▒1,╬▒2), fBT(m,╬▒1,╬▒2) ĻĘĖļ”¼Ļ│Ā fJB(m,╬▒0.54,╬▒0.93,╬▒0.95,╬▒1.95,╬▒2)Ļ░Ć ļÉśĻ│Ā, 2.2ņĀłņŚÉņä£ ļČäņäØĒĢ£ ĻĖ░ņĪ┤ņØś Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖļōżņØĆ
ņ£╝ļĪ£ ļéśļłäļ®┤ fWL(m, ╬▒2) , fDK(m,╬▒1,╬▒2), fBT(m,╬▒1,╬▒2) ĻĘĖļ”¼Ļ│Ā fJB(m,╬▒0.54,╬▒0.93,╬▒0.95,╬▒1.95,╬▒2)Ļ░Ć ļÉśĻ│Ā, 2.2ņĀłņŚÉņä£ ļČäņäØĒĢ£ ĻĖ░ņĪ┤ņØś Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖļōżņØĆ 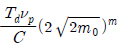 ļź╝ ņĀ£ņÖĖĒĢśļ®┤ S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżļĪ£ ņĪ░ĒĢ®ļÉ£ ļ│Ąņ×ĪĒĢ£ ļŗżĒĢŁņŗØ ļ░Å ĒĢ©ņłśļĪ£ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢ£ Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ņ”ē, Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØĆ ļ│Ąņ×ĪĒĢ£ ļŗżĒĢŁņŗØĻ│╝ ĒĢ©ņłśņØ┤ņ¦Ćļ¦ī ņØ┤ ĒĢ©ņłśļōżņØś ļÅģļ”Įļ│ĆņłśļŖö ļŗ©ņ¦Ć S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżņØ┤ ļÉśļ®░, Ēö╝ļĪ£ņåÉņāüņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ņÜöņåīļŖö S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżļĪ£ ņĀĢĻĘ£ĒÖöņŗ£Ēé¼ ņłś ņ׳ņØīņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļź╝ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØ┤ļØ╝Ļ│Ā ņĀĢņØśĒĢśņśĆņ£╝ļ®░, ņŗØ (33)Ļ│╝ Ļ░ÖņØ┤ ļéśĒāĆļé┤ņŚłļŗż.
ļź╝ ņĀ£ņÖĖĒĢśļ®┤ S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżļĪ£ ņĪ░ĒĢ®ļÉ£ ļ│Ąņ×ĪĒĢ£ ļŗżĒĢŁņŗØ ļ░Å ĒĢ©ņłśļĪ£ Ēö╝ļĪ£ņåÉņāüņØä ņśłņĖĪĒĢ£ Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ņ”ē, Ēö╝ļĪ£ņåÉņāüļ¬©ļŹĖņØĆ ļ│Ąņ×ĪĒĢ£ ļŗżĒĢŁņŗØĻ│╝ ĒĢ©ņłśņØ┤ņ¦Ćļ¦ī ņØ┤ ĒĢ©ņłśļōżņØś ļÅģļ”Įļ│ĆņłśļŖö ļŗ©ņ¦Ć S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżņØ┤ ļÉśļ®░, Ēö╝ļĪ£ņåÉņāüņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ņÜöņåīļŖö S-NĻ│ĪņäĀņØś ĻĖ░ņÜĖĻĖ░ņÖĆ ļ░┤ļō£ĒÅŁ ļ¦żĻ░£ļ│ĆņłśļōżļĪ£ ņĀĢĻĘ£ĒÖöņŗ£Ēé¼ ņłś ņ׳ņØīņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļź╝ ņĀĢĻĘ£ĒÖöļÉ£ Ēö╝ļĪ£ņåÉņāüņØ┤ļØ╝Ļ│Ā ņĀĢņØśĒĢśņśĆņ£╝ļ®░, ņŗØ (33)Ļ│╝ Ļ░ÖņØ┤ ļéśĒāĆļé┤ņŚłļŗż.