|
 |
- Search
| J. Ocean Eng. Technol. > Volume 35(5); 2021 > Article |
|
Abstract
The prediction of wave conditions is crucial in the field of marine and ocean engineering. Hence, this study aims to predict the significant wave height through machine learning (ML), a soft computing method. The adopted metocean data, collected from 2012 to 2020, were obtained from the Korea Institute of Ocean Science and Technology. We adopted the feedforward neural network (FNN) and long-short term memory (LSTM) models to predict significant wave height. Input parameters for the input layer were selected by Pearson correlation coefficients. To obtain the optimized hyperparameter, we conducted a sensitivity study on the window size, node, layer, and activation function. Finally, the significant wave height was predicted using the FNN and LSTM models, by varying the three input parameters and three window sizes. Accordingly, FNN (W48) (i.e., FNN with window size 48) and LSTM (W48) (i.e., LSTM with window size 48) were superior outcomes. The most suitable model for predicting the significant wave height was FNN(W48) owing to its accuracy and calculation time. If the metocean data were further accumulated, the accuracy of the ML model would have improved, and it will be beneficial to predict added resistance by waves when conducting a sea trial test.
Metocean data are essential in the marine industry, such as in the transportation, installation, operation, and survival of offshore structures. They are also adopted to determine the departure time and route of merchant vessels, as well as new renewable energy development projects, and offshore constructions. Shipboard measurements began in 1854 for time-series observations of wind speed and wave height, while marine buoy was introduced in the 1970s for metocean observations. Owing to the emergence of marine observation satellites in the late 1970s, elucidating the phenomena of wind and waves became possible, and approximately 30 years of data covering the entire globe were collected with the steady development of technologies (Meucci et al., 2020). These accumulated measurement data have been harnessed to generate the re-analysis and hindcast data calculated via energy balance equations for wind and waves, including several ocean wave models and mathematical techniques (e.g., the differential equation of wave energy). Furthermore, owing to the consistent advancement of numerical models, predicting metocean conditions worldwide has become possible.
The European Centre for Medium-Range Weather Forecasts and the National Oceanic and Atmospheric Administration are well-known agencies that provide metocean predictions. In addition, the statistical analysis of metocean data enables the prediction of extreme values in extensive return periods (e.g., 10, 20, and 100 years) for the operation and survival of merchant vessels and offshore structures during their life cycle (Park et al., 2020). However, terrain and sea surface wind are required as input conditions when numerical wave models are used. Furthermore, temporal and spatial changes in waves are estimated according to the laws of physics; hence, they do not have a sufficient level of precision to replace the observed data. To address these issues, a study was conducted to estimate wave height through machine learning (ML; Kumar et al., 2018).
Conventionally, to enable computers solve a specific problem, humans digitize (e.g., define functions and assign boundary conditions) this problem using mathematical and statistical techniques. Conversely, using ML, humans provide the machine with information related to the problem they attempt to solve, and the machine learns and decipher the rules for the solution to the problem. That is, ML is a data-driven modeling technology that enables machines to grasp the relationship between the input and output by learning by itself, without adopting any specific mathematical forms to solve the problem. From 1940 to 1950, scientists from various fields began the discussion on the possibility of an artificial brain. However, it was not until 1956 that the term artificial intelligence (AI) was officially used. Afterward, this technology passed through a period of technological renaissance, followed by a period of stagnation. Currently, it is called machine learning, artificial neural network (ANN), or deep learning and is currently being incorporated into various academic and industrial fields. With the enhancements in big data technology and computer performance, ML is expected to continue expanding into other fields at an increasing rate (Haenlein and Kaplan, 2019). LeCun et al. (2015) introduced conventional ML models, such as feedforward neural network (FNN), convolutional neural network (CNN), recurrent neural network (RNN), and long-short term memory (LSTM). They also mentioned that these ML models can be applied in areas ranging from simple regression problems to image and voice recognition, language processing, and the medical industry. Moreover, studies have been conducted to detect oil spills using FNN (Kim and Kim, 2017) and to predict the path of a typhoon (Kim et al., 2019), as well as the volume of goods transported using LSTM (Kim and Lee, 2020).
Jain and Deo (2006) presented previous studies that have utilized FNN in the field of ocean engineering. These studies include metocean (e.g., wave height, wave period, wind speed, and tidal level) predictions, as well as predictions of environmental forces acting on marine structures, damage to offshore structures, ship motions, and hull design. Among them, research that utilizes FNN to predict marine weather at a single location is being actively conducted. Moreover, a study was conducted on predicting wave variables (i.e., significant wave height and wave period) in the near future, using the past wave data measured using a buoy (Deo and Naidu, 1998; Makarynskyy, 2004). A study was also performed on predicting wave variables using FNN (Mandal and Prabaharan, 2006). Furthermore, research was conducted to predict wave variables via FNN, using previously collected wind data (e.g., wind speed and wind direction) at a single location (Deo et al., 2001; Kim, 2020). Malekmohamadi et al. (2011) predicted significant wave heights using various soft computing methods (support vector machines (SVMs), Bayesian networks (BNs), and adaptive neuro-fuzzy inference system (ANFIS)), including FNN. In addition, they demonstrated that FNN produces better results than other models. To improve the accuracy of wave prediction, a hybrid-type model known as an empirical orthogonal function (EOF)-wavelet-neural network, which incorporated the ML model into the conventional statistical method, was proposed (Oh and Suh, 2018). Furthermore, a convolutional long short-term memory (ConvLSTM) model was developed by combining CNN and LSTM models, and the ConvLSTM model was proposed to solve the problem with the prediction of sea surface temperature (Jung et al., 2020). However, to perform ML for metocean predictions, it remains impossible for machines to handle the entire process unassisted. The input data for solving problems, selection of a suitable ML model, and tuning of hyperparameters are crucial in ML. However, human intervention is still required in this process, and it takes a significant amount of trial and error to create a ML model that can make excellent metocean predictions.
This paper proposes a ML model that predicts significant wave heights using the metocean data obtained from an oceanographic buoy at the Korea Strait, which was provided by the Korea Institute of Ocean Science and Technology (KIOST). The types and number of input data were classified into three cases by considering the Pearson correlation coefficient of the collected metocean data. The FNN and LSTM models that have incorporated the concept of window size were adopted as the ML model. The numbers of nodes and layers, including the activation functions for the hidden layer, were varied to derive the combination of hyperparameters that minimize the mean absolute error (MAE) between the predicted and measured values for the validation set. An ML model that predicts significant wave heights using the input variables, as well as the selected hyperparameters and their characteristics, were regarded as the outcome of this study.
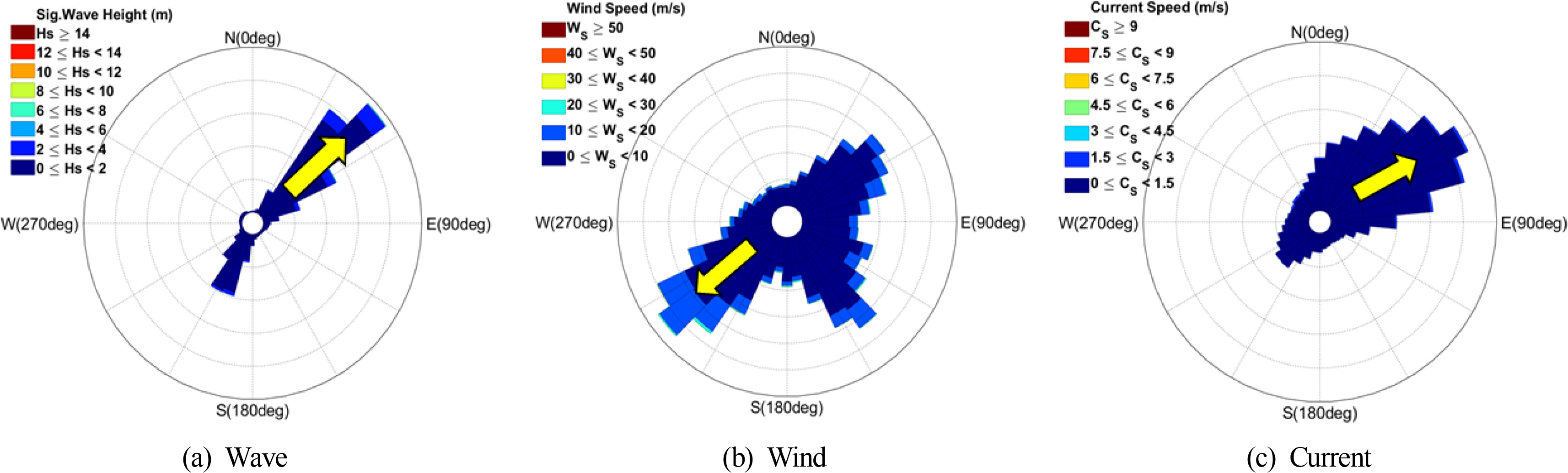
The metocean data were collected from the Korea Strait oceanographic buoy provided by KIOST. The Korea Strait is one of the representative sea areas where sea trials are conducted on domestically built vessels before delivery. Fig. 1 illustrates the location of the Korea Strait oceanographic buoy. Its latitude and longitude are 34°55′0″N and 129°07′16″E, respectively. The Korea Strait oceanographic buoy commenced observations in September 2012 and has been in operation since then. The data adopted in this study span a total period of 9 years (from 2012 to 2020). The collected data comprise 13 categories and is organized in intervals of 30 min. These categories include surface current speed, surface current direction, water temperature, salinity, significant wave height, significant wave period, maximum wave height, maximum wave period, wave direction, wind speed, wind direction, air temperature, and air pressure. For the raw data, approximately 17,500 data sets are measured and stored each year on average, and the total number of data sets over the 9-year period is 157,825. There were outliers in the raw data because of the malfunction of the measuring equipment and facility repairs, owing to bad weather conditions. For time period that contain outliers (‘NaN’, ‘-’, ‘0’, ‘99.99’), all environment variables, including the time period, were discarded from the dataset. Fig. 2 and Table 1 present the number of data for each year for the raw and filtered data from where the outliers have been eliminated. The number of filtered data in 2012 and 2013 is significantly low because the buoy commenced its operation in September 2012, and significant wave height and current information were not stored in 2013 owing to an inherent problem with the measuring equipment. Excluding the data for 2012 and 2013, the amount of usable data is approximately 78% of the total data. The statistical analysis was performed using approximately 98,000 filtered data. Fig. 3 presents the wave scatter diagram(WSD) for the significant wave height and significant wave period, and Fig. 4(a) presents the wave rise with significant wave height and wave direction. In addition, Fig. 4(b) presents the wind rose with the wind speed and wind direction, while Fig. 4(c) illustrates the current rose diagram with the surface current speed and surface current direction.
The WSD presents the frequency of the significant wave height at intervals of 1 m, as well as the frequency of the significant wave period at intervals of 1 s. The wave condition with the most frequency is between 0 m and 1 m for the significant wave height, and between 4 s and 5 s for the significant wave period. The direction the waves, winds, and currents move toward is depicted using a rose diagram and is divided into the east (90°), south (180°), and west (270°), in a clockwise direction from the true north (0°). According to the KIOST, the direction the waves and currents move toward and the direction the wind blows from are defined as the direction of each environmental variable. However, the definition of wind direction was altered to match the definition of wave and current direction and to adopt the direction as an input variable for the ML model. The most dominant directions of wave, wind, and currents in 16 azimuths are the northeast (NE), southwest (SW), and east-northeast (ENE) directions, respectively. For the wind direction, the frequency of the winds blowing toward the southeast (SE) direction is high as well, and it is presumed to be the effect of the northwest wind, which blows during the winter season in Korea.
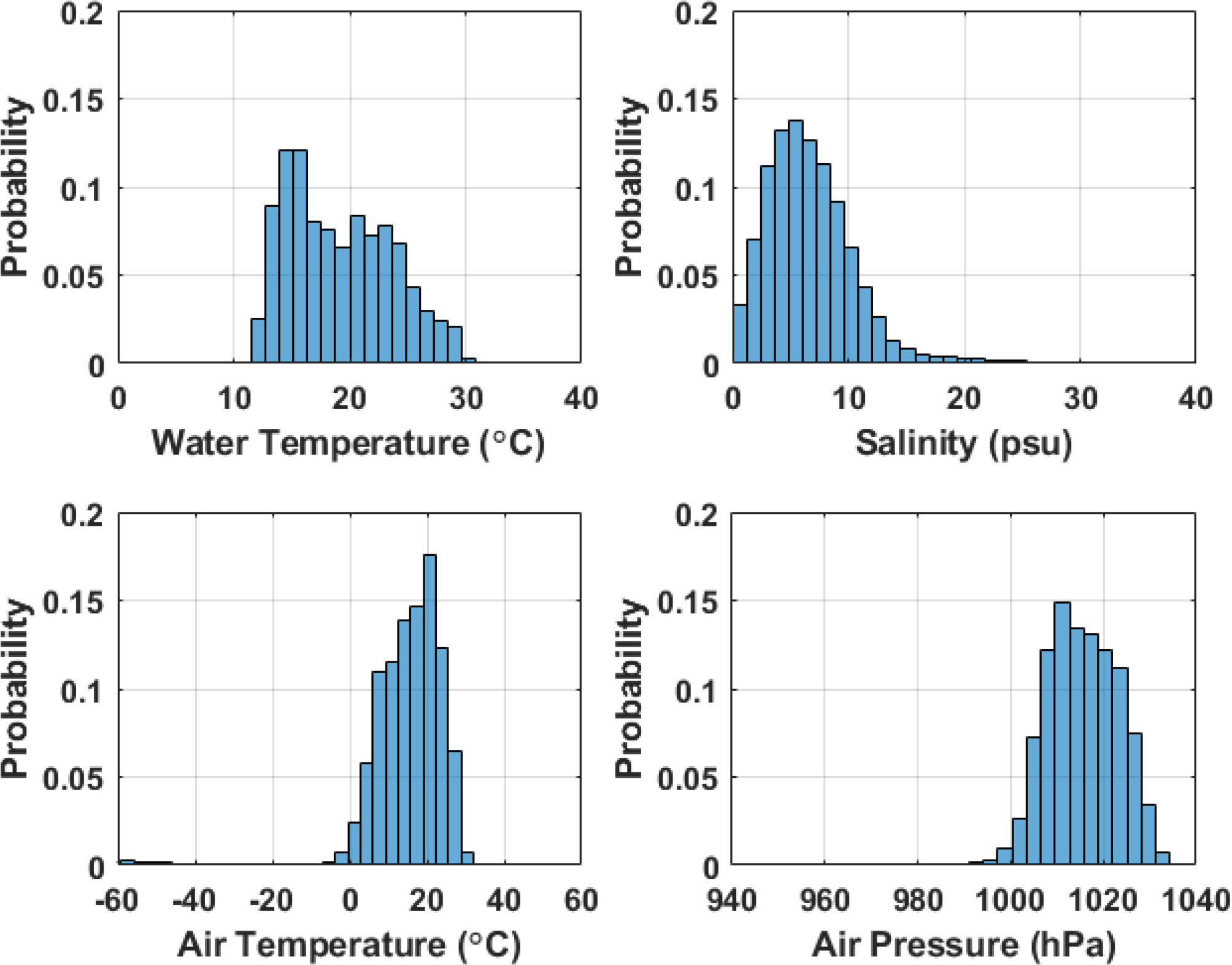
In Fig. 5, the remaining categories, water temperature, salinity, air temperature, and air pressure are presented in histograms, which represent probabilities. The histogram for water temperature presents a uniform distribution, mostly between 10 °C and 30 °C, and the salinity histogram exhibits a unimodal probability distribution at approximately 5 psu. Similarly, the histograms for air temperature and air pressure exhibit unimodal probability distributions at approximately 20 °C and 1010 hPa, respectively. In the air temperature case, an unrealistic temperature of approximately −60 °C was intermittently measured. Nevertheless, it is challenging to determine a reasonable threshold that can distinguish outliers in metocean data. However, an advantage of ML is that a small number of outliers do not have a significant effect on the ML results (Jain and Deo, 2006). Therefore, the existing small number of outliers for air temperature (2% of the total data) was not discarded. Finally, the maximum wave height and maximum wave period were not adopted as input variables in this study; hence, they are not presented separately.
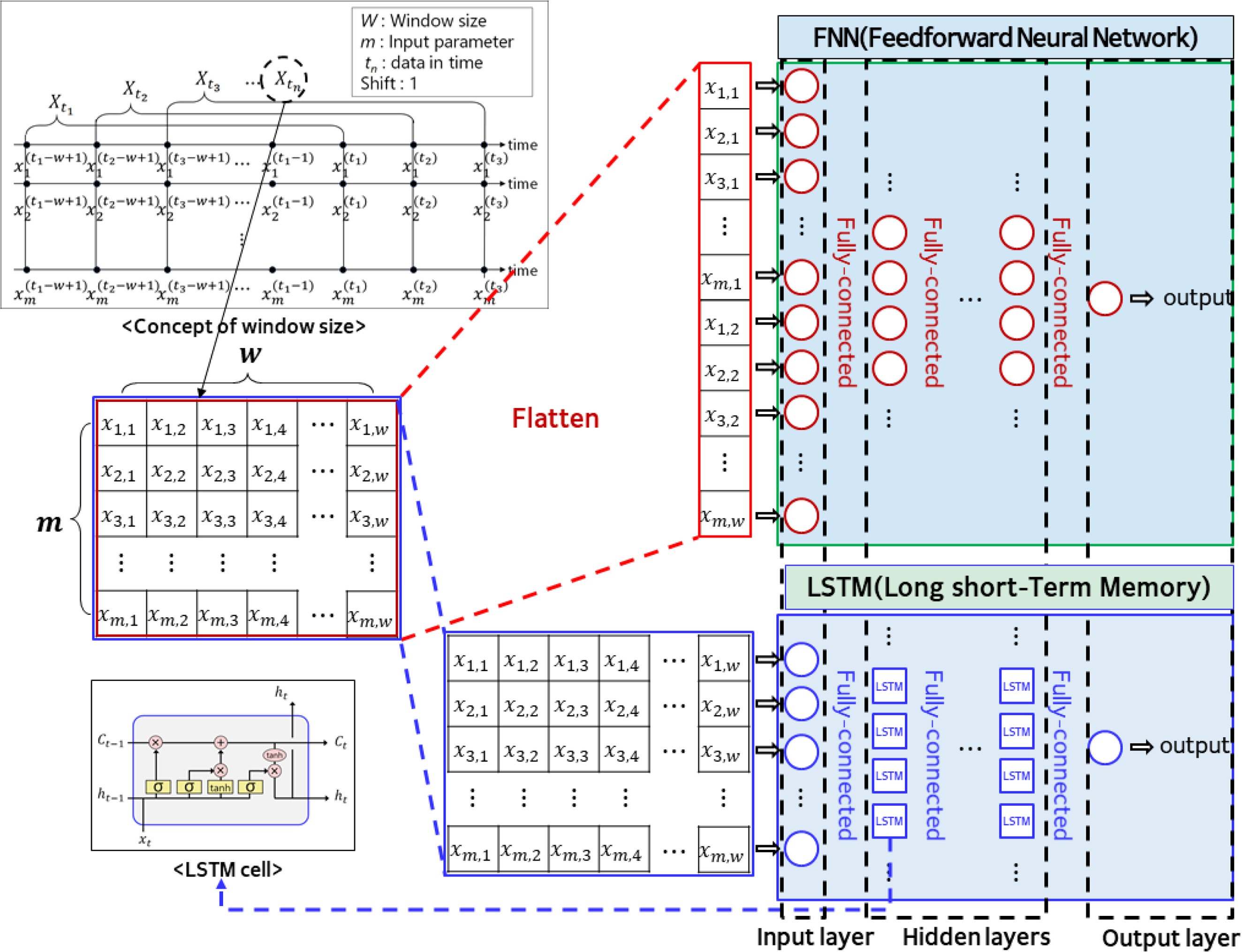
The basic structure of an artificial neural network is created by imitating the human brain, which generates an output when a certain threshold is exceeded at a synapse junction between neurons. In this study, FNN and LSTM were adopted as the ML models. FNN is the simplest ML model that comprises input, hidden, and output layers, and LSTM exhibits an excellent performance in time-series learning. The first FNN layer is an input layer, and the number of nodes in the input layer is set to match the number of input variables. The final layer is the output layer, and it has the same number of nodes as the number of predictor variables. The layers between the input and output layers are called hidden layers, and the product of the input variables and weights are calculated using the arithmetic operation of the activation function. As the number of hidden layers increases, the neural network is called the multi-layer FNN or deep learning.
Datasets are generally classified into a training and a test sets or training, validation, and test sets for machine learning. Recently, the rectified linear unit (ReLU), sigmoid, and hyperbolic tangent (Tanh) functions have been widely adopted as the activation function of hidden layers (LeCun et al., 2015). A linear function is used as the activation function for the output layer when there is no limit on the output value range. The result obtained from the arithmetic operations of the activation function in the output layer is the predicted value, and this value is compared with the measured value. The mean squared error (MSE) or the MAE is often adopted as the error function for this process. ML updates the weights and bias to minimize the error between the predicted and measured values. This process can be performed using an error backpropagation algorithm in a multi-layer neural network. The error backpropagation algorithm progresses from the output layer to the input layer, and it updates the weights and bias values of each layer of the neural network by using the partial derivatives of the error function. In addition, the error backpropagation algorithm can control the learning speed based on the learning rate. If the learning rate is quite high, the global minima cannot be attained. In contrast, the learning slows down if the learning rate is quite low, and the gradient descent falls into the local minima, which prevents it from reaching the global minima. An advanced gradient descent method known as the Adam optimizer is widely adopted in programming. A previous study adopted the concept of momentum to prevent the gradient descent from falling into the local minima, and this method can quickly and accurately determine the point where the differential gradient is the minimum (Cho, 2020).
LSTM is suitable for time-series data because it is configured with a feedback connection. It was devised to address the vanishing gradient or exploding gradient problem of RNN, which has a multi-layered structure. Hochreiter and Schmidhuber (1997) first developed LSTM by altering the internal nodes of the RNN with a complex structure called a memory cell. It was improved by Gers et al. (1999), and the improved version is currently adopted as the ML model. LSTM is similar to FNN; however, the two models differ because three gates and the internal nodes share the same weight in LSTM. The three gates include the input, forget, and output gates, and they play the role of determining the extent to which the input information is memorized and are updated with new results based on this information (Ann, 2016; Jung et al., 2020). The LSTM structure comprises the input, hidden, and output layers. In addition, LSTM updates the weights and bias values using the error backpropagation algorithm to determine the predicted value with the minimum error, relative to the measured value.
FNN and LSTM can both adopt sequence data as an input variable, and the number of sequence data is defined by the window size. Fig. 6 illustrates the FNN and LSTM that have incorporated the concept of window size.
In this study, the ML development environment comprised Python 3.7.10, TensorFlow 2.4.1, and Keras 2.4.0. Significant wave heights were predicted using the FNN that uses data from a single time point as an input, including the FNN and LSTM that have incorporated the concept of window size. The dataset was divided into training, validation, and test sets for the performance evaluation of ML models; in addition, the holdout validation was performed. The proportion of the training (2012–2018), validation (2019), and test (2020) sets is approximately 76:10:14. The sensitivity analysis was conducted based on the changes to the window size for the input data, the number of nodes and layers for the hidden layers, and the activation function (Eqs. (1)–(3)). In addition, the result with the smallest MAE (Eq. (4)) between the predicted and measured values in the validation set was selected as the optimal hyperparameter combination using the Adam optimizer.
In Eq. (4)N, Ŷi, and Yi represent the total number of data points in the dataset, predicted value, and measured value, respectively.
The Pearson correlation coefficient (r) of Eq. (5) was derived for the collected metocean data to select the variables for the input layer of the ML model (Fig. 7).
In Eq. (5)pi and qi represent individual values of the metocean data for calculating the correlation coefficient, while p̄ and q̄ are the average values of the selected metocean data. Here, n denotes the number of metocean data.
The significant wave height (Hs), a predictor variable, was most correlated with the maximum wave height (Hmax), with a correlation coefficient of 0.97. The Hmax was followed by the significant wave period (Ts) and the maximum wave period (Tmax) in the correlation coefficient order. However, the wave data with the same characteristics as the significant wave height were not used as the input data in this study. Instead, in addition to the wave data, the remaining environmental variables were adopted to devise an ML model for predicting the significant wave height. Excluding the wave data, the order of the absolute value of the correlation coefficient, from the highest to lowest, is wind speed, wind direction, current direction, and water temperature. Based on this result, the input variable conditions were divided into three categories in Table 2. In addition, to solve the discontinuity problem with the direction (0°–360°) for the current and wind directions, the method of expressing the direction was changed from the polar coordinate system to the Cartesian coordinate system (x, y), using Eq. (6). Afterward, the current and wind directions were adopted as the input variables (Table 2). The input variables were standardized using the feature scaling method (Eq. (7)). The gradient descent method was optimally applied by making the features of the distribution between the input variables the same.
In Eq. (6), θ denotes the angle, while X in Eq. (7) represents the input variable. In addition, μ and σ represent the mean and standard deviation, respectively. The input variables were categorized into 3, 5, and 10, and the category with three input variables comprised the wind speed and wind direction. This is because wind speed and wind direction are the most important factors for predicting waves in the FNN (Mohjoobi et al., 2008). Therefore, it is determined that estimating the wave height with only wind data is a substantially rational approach. The categories with 5 and 10 input variables were classified to identify the effect of the correlation coefficient between the output and input variables.
The number of nodes and layers in the hidden layers are hyperparameters related to the capacity of the model for the training set. If the capacity is low, underfitting occurs such that errors cannot be sufficiently reduced during the learning process. However, if the model’s capacity is quite high, overfitting may occur, where the model learns patterns that are unrelated to the prediction of the test set. There is no clear standard for determining the number of layers and nodes for the hidden layers corresponding to the input variables. Although several empirical formulas (Huang and Foo, 2002) exist, the optimal hyperparameters need to be determined via repeated experimentations, as well as through trial and error. Therefore, sensitivity analysis was performed on the number of layers and nodes in the hidden layers, and the test matrix is presented in Table 3. The Adam optimizer and MAE were adopted as the optimizer and error function, respectively, while the number of batches and epochs were fixed at 256 and 200, respectively. To prevent overfitting, the early stopping technique was applied to stop the learning when the validation error reaches the minimum value in the iterative learning process. In addition, the learning rate was set to 0.001 (Kingma and Ba, 2014), and a linear function was used as the activation function for the output layer.
A total of 720 FNN and LSTM models were generated based on the changes to the hyperparameters, and training was performed on each model. The MAE between the predicted and measured values of the validation set was compared for each epoch, and the lowest result was selected as the representative value. Among the 720 calculated results, the combination with the smallest MAE was selected as the optimal hyperparameter.
The FNN (W1), which was trained with the training set comprising the input and predictor variables at a single time point, was selected as the baseline performance. From each ML model, the FNN (W48) and LSTM (W48), with a window size of 48 (1 day) each, had the lowest MAE for the corresponding hyperparameters (Table 4).
Significant wave heights were predicted using three types of ML models (i.e., FNN (W1), FNN (W48), LSTM (W48)), three cases of input variables (i.e., 3, 5, 10), and a combination of the optimal hyperparameters (Table 4). The ML models were evaluated using the test set. The predicted values calculated by inputting the input variables of the test set and the predictors in the test set were compared using a time-series graph and a histogram.
Fig. 8 presents time-series graphs for the three methods of the ML model and three conditions for input variables. In addition, the MAE between the predicted and measured values is presented in the upper-right corner of each graph. In general, the calculated MAE of the model with only the wind variable (input variable 3) was the smallest. Furthermore, it can be observed that the FNN (W48) and LSTM (W48) with window sizes of 48 each generated better results than FNN (W1). Kim (2020) predicted the significant wave heights through FNN (W1) using the wind speed, wind direction, and wave direction data from the data collected by the Oeyeondo oceanographic buoy and obtained outstanding results with a MAE of 0.283 m. It is presumed that outstanding results could be obtained using only the FNN (W1) because the wind speed, which was adopted as the input variable, was highly correlated (r > 0.8) with the significant wave height. In the FNN (W48), the MAE tends to increase as the number of input variables gradually increases. However, the input variables (5 and 10) yield the same MAE in the case of the LSTM (W48).
To check the frequency of the predicted values relative to the measured values for each wave height, the probability histogram of two values for the significant wave height is presented in Fig. 9. The graphs on the left-hand side show the probability histogram for the entire data of each ML model. The graphs on the right-hand side present magnified histograms for the data with a significant wave height of 2 m or higher, which have low probability. In FNN (W1), the predicted values have a higher frequency than the measured values around the significant wave height of 0.6 m, where the frequency of the measured values is the highest. In contrast, the predicted values have a lower frequency than the measured values for a wave height of 2 m or higher. For both the FNN (W48) and LSTM (W48) models, the predicted values at approximately 0.6 m, where the frequency of the measured values is the highest, exhibit a frequency similar to the measured values. Although the probability of the occurrence of a high wave (with height of 5 m or higher) is low for the measured values, it was verified that a difference exists between the measured and predicted values in the area where the wave height is 5 m or higher for all three ML models.
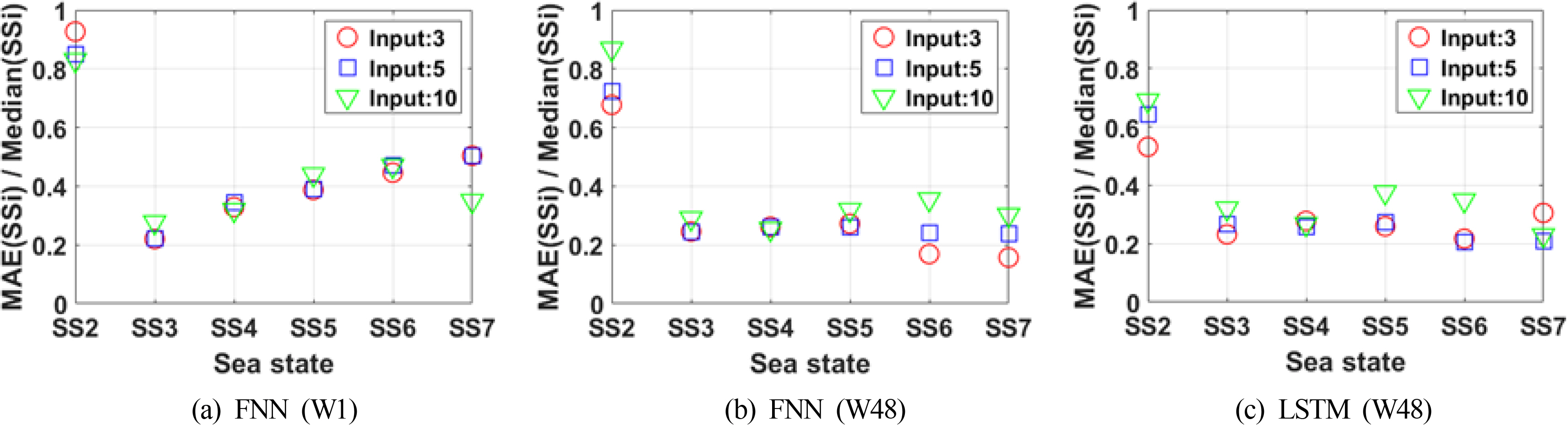
Finally, the difference between the predicted and the measured values was analyzed by introducing the concept of the sea state (SS). The SS code, which the World Meteorological Organization (WMO) classified into grades 0–9, was adopted (Table 5). Significant wave heights of the measured values used as the test set are distributed between the SS2 grade and the SS7 grade, as provided by the WMO. The MAE between the predicted and the measured values in each SS range was nondimensionalized by the median of the corresponding SS, and its results are presented in Fig. 10.
In general, the result of input variable 3, which solely adopted wind as the input variable, exhibits a smaller MAE value, compared to those of input variables 5 and 10. Using the variable with a correlation coefficient greater than 0.1 (input variable 5) yields the second-best result. Contrary to our expectations, a relatively large error was generated when the results were calculated by adding water temperature, salinity, air temperature, and air pressure, compared to using input variables 3 and 5. It is presumed that variables that have low correlation coefficients but with the significant wave height are recognized as noise during training, and they cause overfitting. In the FNN (W1), it can be verified that the difference between the predicted and measured values tend to increase steadily as the significant wave height of the measured value gradually increases according to the SS. The LSTM (W48) model exhibits better prediction performance than the other two models for the SS2 grade of low wave heights. However, excluding the results for the SS2 grade with relatively low absolute error, it is determined that the FNN (W48) with input variable 3 is the best prediction model. In addition, the FNN (W48) model exhibit a higher prediction accuracy than the LSTM (W48) model for the SS6 and SS7 grades, and its computation speed is more than twice as fast. Therefore, considering the prediction accuracy and computation time, the FNN (W48) is proposed as a model for predicting significant wave heights in the Korea Strait.
In this paper, an ML model for predicting significant wave heights was proposed using the metocean data collected from the Korea Strait oceanographic buoy of KIOST. The ML model adopted FNN and LSTM network models. Based on the Pearson correlation analysis between the metocean data, three cases of input variables were selected. In addition, the hyperparameter combination with the minimum MAE was obtained via the sensitivity analysis of the window size, number of nodes in the hidden layers, number of layers, and activation function. The Adam optimizer was adopted as the optimizer in this process, and the number of batches and epochs were fixed at 256 and 200, respectively. Significant wave height prediction results of the FNN (W1) with a window size of 1 (30 min), the FNN (W48) with a window size of 48 (1 day), and the LSTM (W48) with a window size of 48 were compared with the measured values using time-series charts and histograms. In addition, the SS code was incorporated to compare the MAE nondimensionalized by the median of each SS for each model and input variable. The MAE of the prediction results was the smallest when the input variables solely comprised wind data. When environment variables that exhibit negligible correlation with the significant wave height (r < 0.1) were adopted, the MAE exhibited a tendency to increase. In the comparison of the FNN (W1) and the FNN (W48), which are the same FNN models, the FNN (W48) exhibited a smaller MAE for the test set. In the comparison between the FNN (W48) and LSTM (W48), using two models with the same window size, the LSTM (W48) exhibited a slightly smaller mean absolute error for the test set. However, when the MAE was compared based on the SS, the FNN (W48) with input variable 3 demonstrated better results between the SS3 and SS7 grades, except for the SS2 grade. In addition, the FNN (W48) was twice as fast as the LSTM (W48) in terms of computation time. Therefore, by comprehensively considering factors such as the accuracy of significant wave height predictions and computation speed, the FNN (W48) was evaluated to be the suitable ML model for predicting significant wave heights in the Korea Strait. When predicting significant wave heights, selecting input variables using correlation coefficients can produce outstanding results in machine learning. In addition, it is determined that optimal prediction models can be created using only wind data (e.g., wind speed and wind direction). However, the prediction accuracy was slightly lower in high wave areas with a significant wave height of 4 m or higher. It is inferred that the high wave prediction exhibits lower performance because the amount of high-wave data owing to typhoons is insufficient. To address this problem, it is necessary to expand the high-wave data when typhoons occur or develop an ML model that efficiently utilizes limited high-wave data. Finally, The ML model that predicts significant wave heights using only wind data can be utilized at the practical work where is adjusting the engine’s power considering the added resistance of the ship, owing to the waves according to the SS, during sea trials. In the future, we plan to continue our research and enhance the accuracy of the model for predicting significant wave heights in the Korea Strait by adopting the data obtained from other oceanographic buoys near the Korea Strait oceanographic buoy, or the hindcast data, as input variables.
Funding
This study was supported by the following technology innovation programs: of “R&D Platform Establishment of Eco-Friendly Hydrogen Propulsion Ship Program (No. 20006636)” and “the Global Advanced Engineer Education Program for Future Ocean Structures (P0012646)”, which were funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea).
Fig. 1
Location of Korea Strait oceanographic buoy (Korea Institute of Ocean Science and Technology (KIOST), 2021)
Fig. 8
Comparison between the measured and predicted values in time series varied with input nodes and ML models
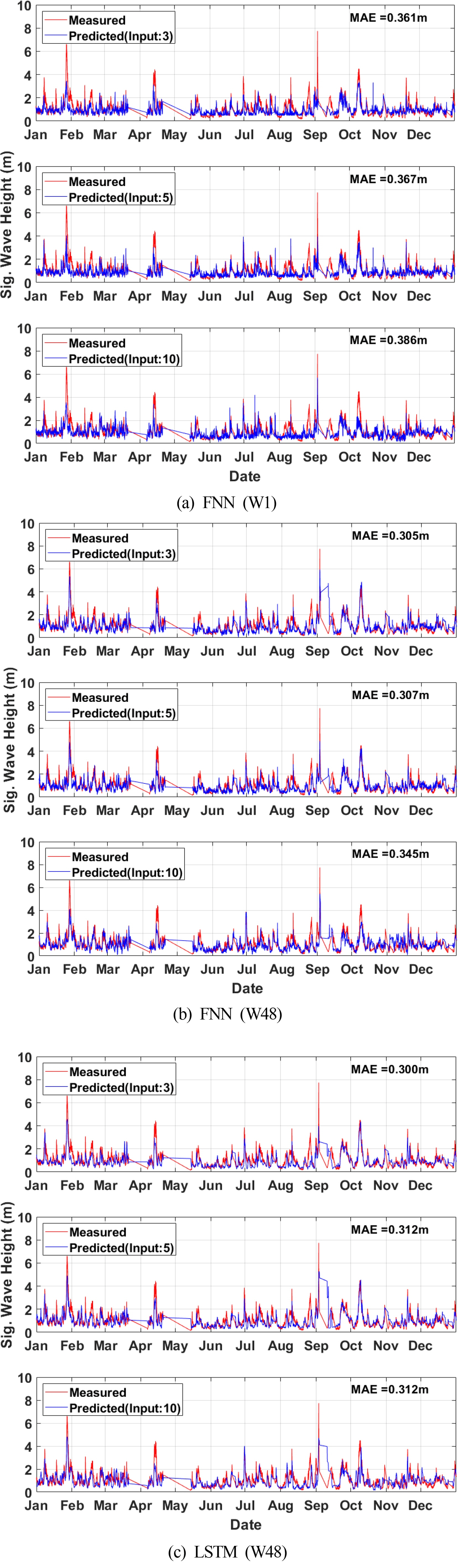
Fig. 9
Comparison between the measured and predicted values varied with input nodes and ML models using the histogram
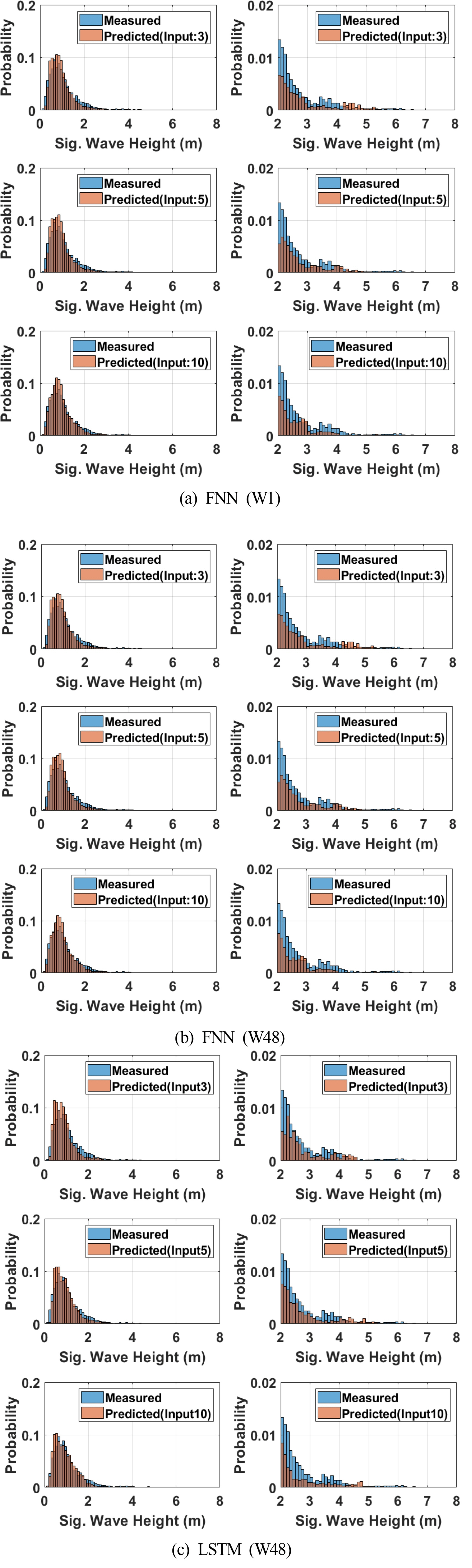
Table 1
Data availability of metocean data of Korea Strait oceanographic buoy
Table 2
Input variables for the input layer
Table 3
Test matrix for the sensitivity analysis
Table 4
Summary of ML models and hyperparameter
Table 5
WMO sea state code (3700) (WMO, 2019)
References
Ahn, S. (2016). Deep Learning Architectures and Applications. Journal of Intelligence and Information Systems, 22(2), 127-142.

Cho, T. (2020). Deep Searning for Everyone (2nd ed.). Gibut, ISBN 979-11-6521-039-7, 368.
Deo, MC., Jha, A., Chaphekar, AS., & Ravikant, K. (2001). Neural Networks for Wave Forecasting. Ocean Engineering, 28(7), 889-898.

Deo, MC., & Naidu, CS. (1998). Real Time Wave Forecasting Using Neural Networks. Ocean Engineering, 26(3), 191-203.

Gers, FA., Schmidhuber, J., & Cummins, F. (1999). Learning to Forget: Continual Prediction with LSTM.
Haenlein, M., & Kaplan, A. (2019). A Brief history of Artificial Intelligence: On the Past, Present, and Future of Artificial Intelligence. California management review, 61(4), 5-14.

Hochreiter, S., & Schmidhuber, J. (1997). Long Short-term Memory. Neural Computation, 9(8), 1735-1780.


Huang, W., & Foo, S. (2002). Neural Network Modeling of Salinity Variation in Apalachicola River. Water Research, 36(1), 356-362.


Jain, P., & Deo, MC. (2006). Neural Networks in Ocean Engineering. Ships and Offshore Structures, 1(1), 25-35.

Jung, S., Kim, YJ., Park, S., & Im, J. (2020). Prediction of Sea Surface Temperature and Detection of Ocean Heat Wave in the South Sea of Korea Using Time-series Deep-learning Approaches. Korean Journal of Remote Sensing, 36(5‒3), 1077-1093.
Kim, DH., & Lee, K. (2020). Forecasting the Container Volumes of Busan Port Using LSTM. Journal of Korea Port Economic Association, 36(2), 53-62.

Kim, GD., & Kim, YH. (2017). A Survey on Oil Spill and Weather Forecast Using Machine Learning Based on Neural Networks and Statistical Method.
Kim, TY. (2020). A Study on the Prediction Technique for Wind and Wave Using Deep Learning. Journal of the Korean Society for Marine Environment & Energy, 23(3), 142-147.

Kim, YJ., Kim, TW., Yoon, JS., & Kim, IH. (2019). Study on Prediction of Similar Typhoons through Neural Network Optimization. Journal of Ocean Engineering and Technology, 33(5), 427-434.

Kingma, DP., & Ba, J. (2014). Adam: A Method for Stochastic Optimization. arXiv Preprint arXiv, 1412, 6980.
Korea Institute of Ocean Science and Technology (KIOST). (2021). Location of Korea Strait Oceanographic Buoy. Retrieved 17 April 2021 from http://www.khoa.go.kr/oceangrid/khoa/koofs.do
Kumar, NK., Savitha, R., & Al Mamun, A. (2018). Ocean Wave Height Prediction Using Ensemble of Extreme Learning Machine. Neurocomputing, 277, 12-20.

Mahjoobi, J., Etemad-Shahidi, A., & Kazeminezhad, MH. (2008). Hindcasting of Wave Parameters Using Different Soft Computing Methods. Applied Ocean Research, 30(1), 28-36.

Makarynskyy, O. (2004). Improving Wave Predictions with Artificial Ueural Networks. Ocean Engineering, 31(5‒6), 709-724.

Malekmohamadi, I., Bazargan-Lari, MR., Kerachian, R., Nikoo, MR., & Fallahnia, M. (2011). Evaluating the Efficacy of SVMs, BNs, ANNs and ANFIS in Wave Height Prediction. Ocean Engineering, 38(2‒3), 487-497.

Mandal, S., & Prabaharan, N. (2006). Ocean Wave Forecasting Using Recurrent Neural Networks. Ocean Engineering, 33(10), 1401-1410.

Meucci, A., Young, IR., Aarnes, OJ., & Breivik, Ø. (2020). Comparison of Wind Speed and Wave Height Trends from Twentieth-century Models and Satellite Altimeters. Journal of Climate, 33(2), 611-624.

Oh, J., & Suh, KD. (2018). Real-time Forecasting of Wave Heights Using EOF–wavelet–neural Network Hybrid Model. Ocean Engineering, 150, 48-59.

Park, SB., Shin, SY., Jung, KH., Choi, YH., Lee, J., & Lee, SJ. (2020). Extreme Value Analysis of Metocean Data for Barents Sea. Journal of Ocean Engineering and Technology, 34(1), 26-36.

World Meteorological Organization (WMO). (2019). Manual on Codes: International Codes I. 1 part A—Alphanumeric Codes.
- TOOLS
-
METRICS

-
- 6 Crossref
- Scopus
- 6,563 View
- 184 Download
- Related articles in JOET
-
The Prediction of Water Quality in Ulsan Area Using Material Cycle Model2006 February;20(1)
Development of a Wave Monitoring System Using a Marine Radar2006 February;20(1)