Higher-order Spectral Method for Regular and Irregular Wave Simulations

2.1 Mathematical Formulation

In this study, a rectangular fluid domain with a horizontal length L and constant depth h was considered in a Cartesian coordinate system. In this coordinate system, the mean water surface was on the x-axis while the vertical z-axis was directed upwards. Assuming that the fluid is incompressible and inviscid and the flow is irrotational, the velocity of the fluid defined as the gradient of the velocity potential ϕ and the continuity equation, which is the governing equation, is transformed into the Laplace equation as expressed in Eq. (1).

where, ∇ denotes a horizontal gradient operator. According to the study conducted by Zakharov (1968), the surface potential φ^s at the free surface ζ can be defined by Eq. (2).

Using the surface potential φ^s, the kinematic boundary conditions and dynamic boundary conditions of the free surface can be expressed by Eqs. (3)–(4).

where, g and W denote the acceleration due to the gravitational acceleration and vertical velocity of the free surface expressed in Eq. (5), respectively.

The vertical velocity W can be calculated using the HOS model presented by Dommermuth and Yue (1987) and West et al. (1987). The free surface ζ and surface potential φ^s based on to time progress can be obtained by integrating Eqs. (3)–(4), which substitutes the calculated vertical velocity W. It is assumed that the horizontal region is infinite in the HOS model and the periodic boundary condition is adopted as expressed in Eq. (6).

Eq. (7) was adopted in terms of the bottom boundary condition, which is the no-penetration condition condition.

The velocity potential, which is the solution of the Laplace equation that satisfies the aforementioned free surface boundary condition (Eqs. (3)–(4)), lateral periodic boundary condition (Eq. (6)), and bottom boundary condition (Eq. (7)), can be defined by Eq. (8) using a Fourier pseudo-spectral basis.

where, C_m denotes the time-dependent Fourier coefficient of the velocity potential, and k_m denotes wave number defined by Eq. (9), respectively.

Similar to the velocity potential, the surface potential φ^s and free surface ζ can be defined by a Fourier pseudo-spectral basis as expressed in Eqs. (10)–(11).

Where, A_m and B_m respectively denote the time-dependent Fourier coefficients of the surface potential and free surface. The expansions of the surface potential and free surface in Eqs. (10)–(11) were limited to the number of points in the free surface that define the physical quantity. Moreover, the Fourier expansion in Eqs. (10)–(11) provided a horizontal differential to the time integrations of the surface potential and free surface using Eqs. (3)–(4). However, because the vertical velocity W on the free surface is unknown, the vertical velocity W of the free surface can be measured using the HOS model according to the expansion of Dommermuth and Yue (1987). In the HOS model, the surface potential φ^s, which is the physical quantity of the surface, and the free surface ζ were used to evaluate the vertical velocity W of the free surface. First, the velocity potential ϕ can be expressed up to the given order of M with the perturbation expansion for wave steepness as expressed in Eq. (12). where, the perturbation potential ϕ^(m) has a perturbation order of m for the wave steepness. From the mean depth of z = 0, the perturbation potential ϕ^(m) for the free surface can be expressed by Eq. (13) using the expansion of Taylor series.

The vertical velocity W can also be expressed with perturbation expansion as in Eq. (14), as presented in Eq. (12).

where, the vertical perturbation velocity W^(m) also has a perturbation order of m for the wave steepness and the vertical perturbation velocity W^(m) for the free surface ζ from the mean depth of z = 0 can be expressed with Taylor expansion as expressed in Eq. (15).

The perturbation vertical velocity W^(m) in Eq. (15) was calculated via the perturbation velocity potential ϕ^(m), which can be used to measure the vertical velocity W at ζ using Eq. (14).

2.2 Numerical Technique

In this study, the free surface ζ and surface potential φ^s can be predicted depending on time integration using Eqs. (3)–(4), which define the boundary conditions of the free surface. As for time integration, the fourth order Runge–Kutta method, which ensured stability, was adopted as presented by Dommermuth and Yue (1987). The physical quantity and vertical velocity W of the spatial differential included in the boundary condition of the free surface were calculated by applying the FFT algorithm. In this study, a numerical technique was implemented using MATLAB (Matrix laboratory). Because it supports the FFT algorithm and multi-thread, MATLAB provides fast computation. Regarding the HOS method, the multiplication of the nonlinear free surface boundary conditions was performed in a physical space rather than a spectra space. Although such transformation is efficiently performed using FFT, it leads to an aliasing phenomenon. It is therefore imperative to clearly eliminate the aliasing phenomenon to ensure the stability of the analysis owing to its influence on numerical stability. In this study, the zero-padding method was used to eliminate the aliasing phenomenon. Zero padding is a method for performing multiplication operations without aliasing in the physical space by filling in zero to expand the spectral space prior to multiplication. This is accompanied by the expansion of the spectral space, leading to an increase in computational cost as the consequence of an increase in the calculation domain. Therefore, appropriate spatial expansion was achieved via the half-rule as expressed in Eq. (16) (Canuto et al., 1988; Gatin et al., 2017).

where, N_Extend and N represent an extended space for zero padding and the number of free modes used in HOS simulation. The parameter p is completely independent of the aliasing phenomenon when the order M is selected. An increase in computational cost owing to the expansion of the aforementioned spectral space can be expected as the order M increases, as expressed in Eq. (16). In this study, the full de-aliasing(p = M) was adopted because only two-dimensional calculations were performed.

The analysis of the HOS simulation is generally performed from the initial conditions of free surface ζ and surface potential φ^s at the free surface, in which the initialization is known to have significant influence on the numerical stability. According to the study by Dommermuth (2000), the simulation of the HOS method under the linear initial condition causes numerical instability because it does not satisfy the nonlinear free surface boundary conditions in Eqs. (3) and (4). Therefore, Dommermuth (2000) proposed an adjustment scheme to initiate the linear initial condition to the nonlinear free surface condition. This scheme enables the smooth transformation of the nonlinear solution via the relaxation of the nonlinear term of the free surface against time. Eqs. (17)–(18) express the free surface condition to which the relaxation of the nonlinear term was applied by introducing the relaxation time T_a and relaxation index n proposed by Dommermuth (2000).

In this study, the linear free surface ζ_1st and linear potential ϕ_1st were adopted as the initial conditions of the regular wave under deep sea conditions, as expressed in Eqs. (19)–(20).

where, A₀, k, and ω denote the wave amplitude, wave number, and wave frequency of the linear solution. Concerning the initial condition of the irregular wave simulation, the free surface and linear potential of the irregular wave for the space can be defined by using the superposition of linear components. The wave amplitude for the wave frequency constituting the irregular wave from the defined wave spectrum S(ω) can be calculated using Eq. (21).

By substituting the calculated wave amplitude A_i into Eqs. (22)–(23), the initial conditions for the irregular wave simulation, ζ_irregular and φ_irregular can be calculated.

where ∊_idenotes a uniform random number between zero and 2π, and the wave number k_i and wave frequency ω_i are calculated via the dispersion relation. In this study, the joint North Sea wave project (JONSWAP) spectrum (DNV, 2010) was used to define the wave spectrum, as expressed in Eq. (24) where H_s, T_p = 2π/ω_p, γ, and A_γ denote a significant height, peak period, peak shape parameter, and normalizing factor, respectively. Furthermore, σ is a spectral width parameter, which is determined depending on the peak wave frequency ω_p.

3.1 Adjusted Simulation of Single Wave

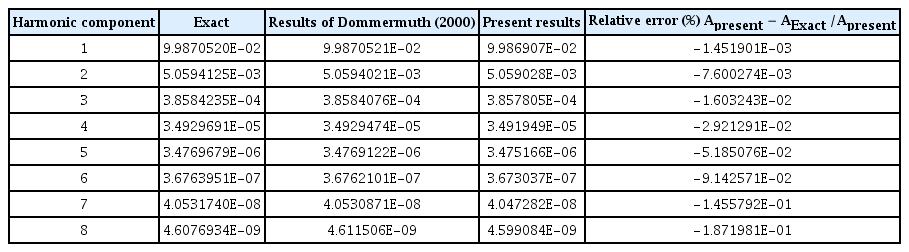
According to the study by Dommermuth (2000), when a linear solution is used as the initial condition and relaxation is applied to the HOS method for a certain period of time, it adjusts to a nonlinear solution. Dommermuth (2000) performed an adjustment simulation at a wave steepness of kA = 0.1 and presented the convergence result of the eighth harmonic component of the Stokes wave. In this study, the developed code was verified by performing calculation conditions, as presented in Table 1, which are the same conditions as those of Dommermuth (2000); after that, the results were compared.

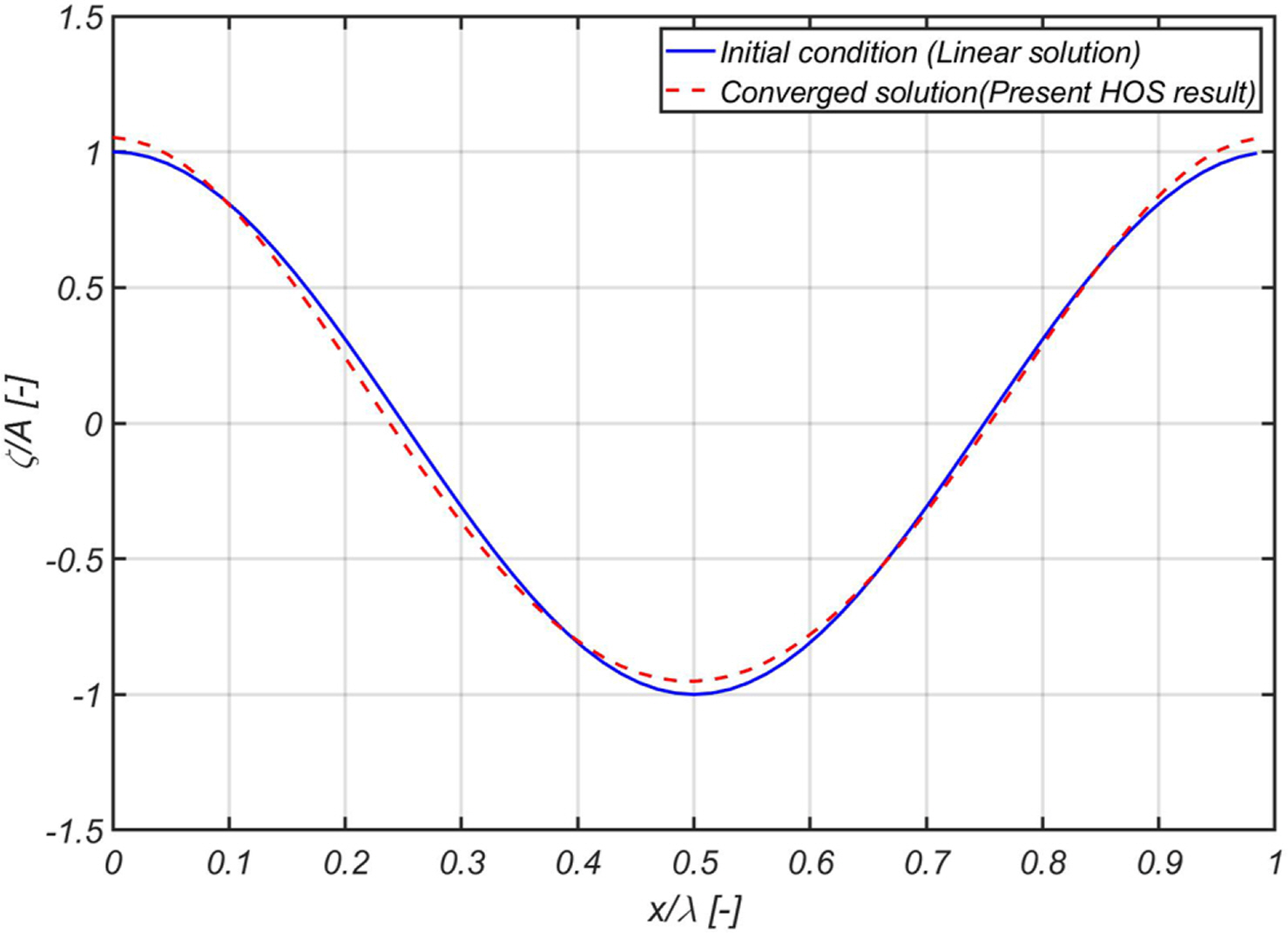
Similar to the study by Dommermuth (2000), a single wave adjustment simulation was performed using 64 modes for 200 seconds with a time step Δt  at 0.025 intervals. In the HOS simulation, the linear solution converged to a nonlinear Stokes wave, as illustrated in Fig. 1.

It was determined that the eight harmonic components of the eighth order Stokes wave converged over time and that the convergence pattern of each harmonic component was similar to the results obtained by Dommermuth (2000), as illustrated in Fig. 2.

The converged results were compared with the analysis solution, as well as the results obtained by Dommermuth (2000), as presented in Table 2. Compared to the analysis solution, it was inferred that the relative error of the code developed in this study was insignificant at less than approximately 0.1%. The validity of the developed code was verified via this result.

3.2 Irregular Wave Simulation

An irregular wave simulation was performed to understand the characteristics of the HOS method. Analysis conditions were defined with reference to the analysis case of Ducrozet et al. (2016), as presented in Table 3. The corresponding condition was a mean steepness of ( smean=kpHs/(22)) 0.1, where nonlinearity exists on the free surface

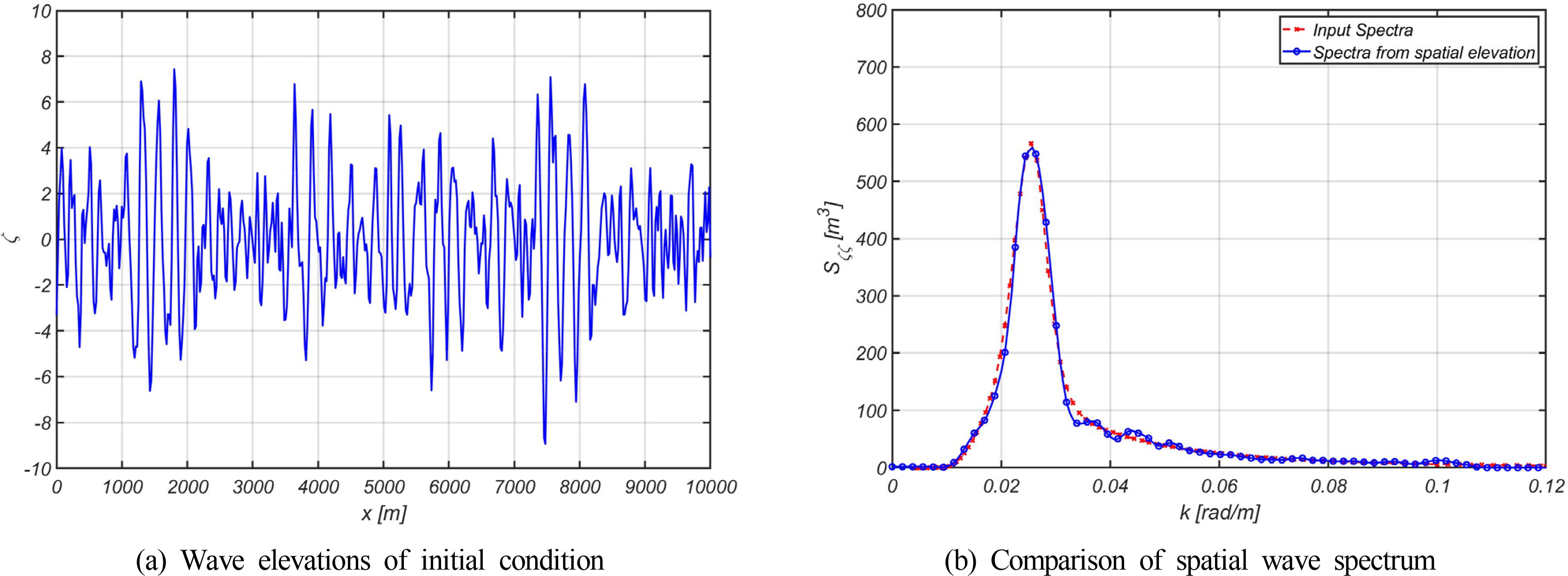
The initial conditions of the irregular wave for this case can be created using Eqs. (22)–(23), as illustrated in Fig. 3(a).

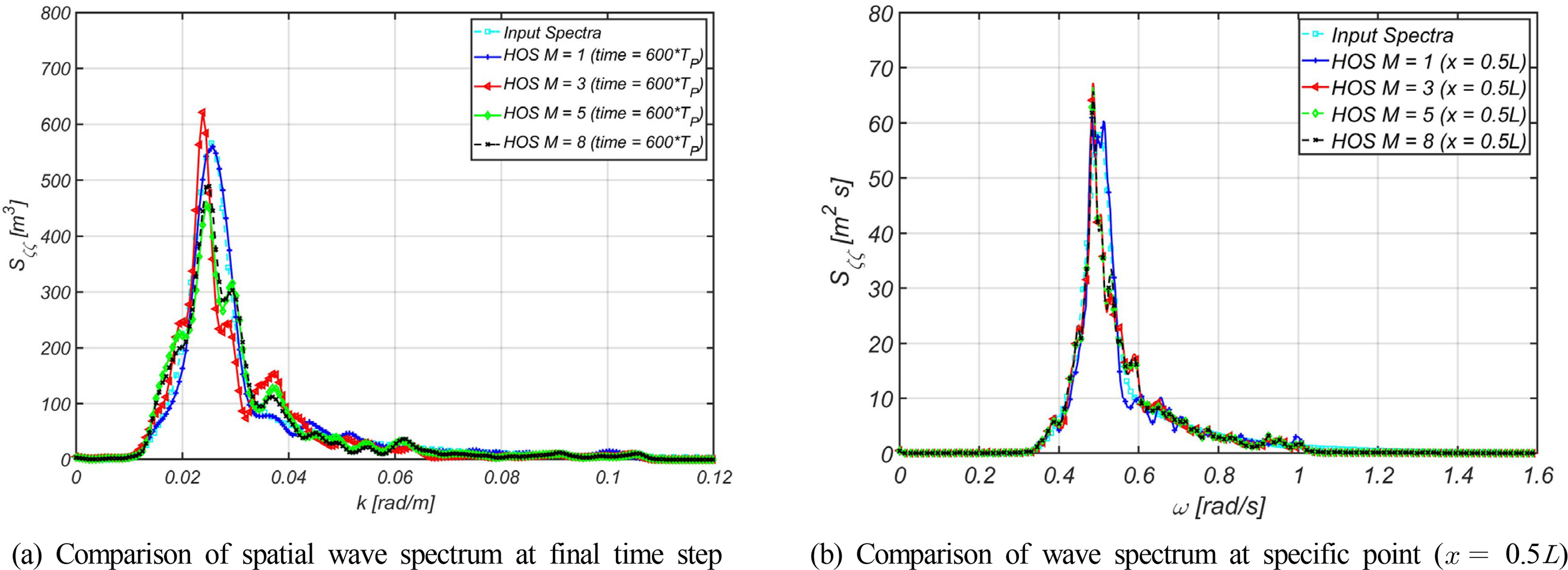
The spatial wave spectrum, obtained from the wave distribution generated, and the input wave spectrum were compared, as illustrated in Fig. 3(b). The two spectra exhibited satisfactory agreement, thus validating the generated wave distribution. The boundary condition at both ends was periodic and the wave from 10 000 m was re-introduced at 0 m when the simulation was performed. Therefore, the HOS method can efficiently simulate the development of irregular waves over a long period of time within a limited spatial grid.

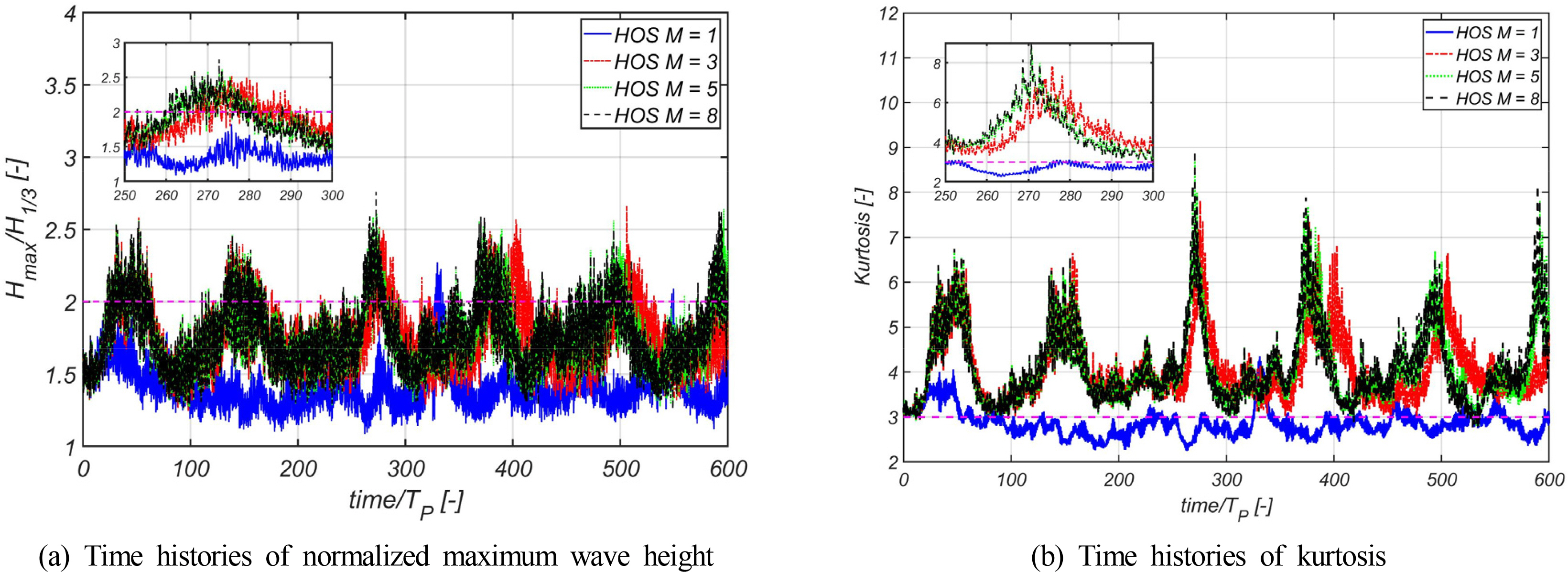
In this study, simulation was performed by varying the order M to 1, 3, 5, and 8 for the same initial condition. Fig. 4 presents the normalized maximum wave height and kurtosis (κ) based on the change in time. When the normalized maximum wave height exceeds 2 m, it is called an abnormality index (AI). It is known that the abnormality index and kurtosis are highly correlated with the occurrence of Freak wave (Kim, 2019). The abnormality index was calculated using H_max and H_1/3 was determined via the zero crossing analysis of the wave distribution at every time step. The kurtosis was a measure adopted to statistically establish the difference with the normal distribution, as defined in Eq. (25).

where σ_ζ and ζ_mean denote the root mean square (RMS) of the spatial wave distribution of the wave height and the mean of the spatial wave distribution, respectively. It was inferred that as time progresses, a significant difference exists between the abnormality index and kurtosis of orders 3, 5, and 8 that reflect the nonlinear effect of the free surface when the order is one, as illustrated in Fig. 4. This phenomenon occurs because of the nonlinear interaction between the wave components. Although the abnormality index and kurtosis of orders 3, 5, and 8 developed similarly up to 260 T_P, the abnormality index and kurtosis of orders 5 and 8 exhibited different results from that of order 3 after 260 T_P. This indirectly showed that the order needs to be 5 or above when simulating 260 T_P or above of the corresponding condition. Moreover, it was inferred that the normalized maximum wave height and kurtosis developed in a similar pattern, thus indicating that the two physical quantities are highly correlated.

The spatial wave spectrum was compared at the final time step, as illustrated in Fig. 5(a). The spectrum represents the distribution of energy, and the change in the spectrum indicates the change in energy distribution. Therefore, from the change in the magnitude of the spectrum of the corresponding wave number, it can be inferred that it was redistributed to the energy of other wave numbers. In the linear free surface boundary condition of order 1, it was concluded that the spatial wave spectrum is approximately similar to the initial value, thus indicating that the energy distribution between the components of the wave remains unchanged. However, the spatial wave spectra of orders 3, 5, and 8 exhibited different results from the initial values. This could be attributed to the nonlinear interaction between the wave components owing to the nonlinear free surface boundary condition, subsequently, it can be inferred that the wave energy was redistributed between the wave components. The wave displacement over time at the center point of the simulation domain was transformed into a spectrum, as illustrated in Fig. 5(b). It was similar to the initial value in the calculation condition of order 1, thus indicating the absence of interactions between wave components. However, the wave spectrum was different from the initial spectrum under the calculation conditions of orders 3, 5, and 8, which is also attributed to the nonlinear interaction between the wave components, and allows us to infer that the energy between the wave components was redistributed. From these results, it was determined that the irregular wave simulation using the HOS method is a satisfactory numerical tool for observing the nonlinear interaction between wave components. As earlier mentioned, it was concluded that the conventional HOS method has the advantage of the long-time simulation for the initial conditions given as periodic boundary conditions at both ends. However, there are limitations to this simulation in that waves are generated only in a limited space and at a specific point, such as in a test tank. A separate numerical technique is required to generate and simulate waves as in a test tank. In the following chapter, a numerical technique for the simulation of wave generation is described. The technique was verified and its characteristics were identified via numerical tests.

4.1 Numerical Techniques for Generating Waves

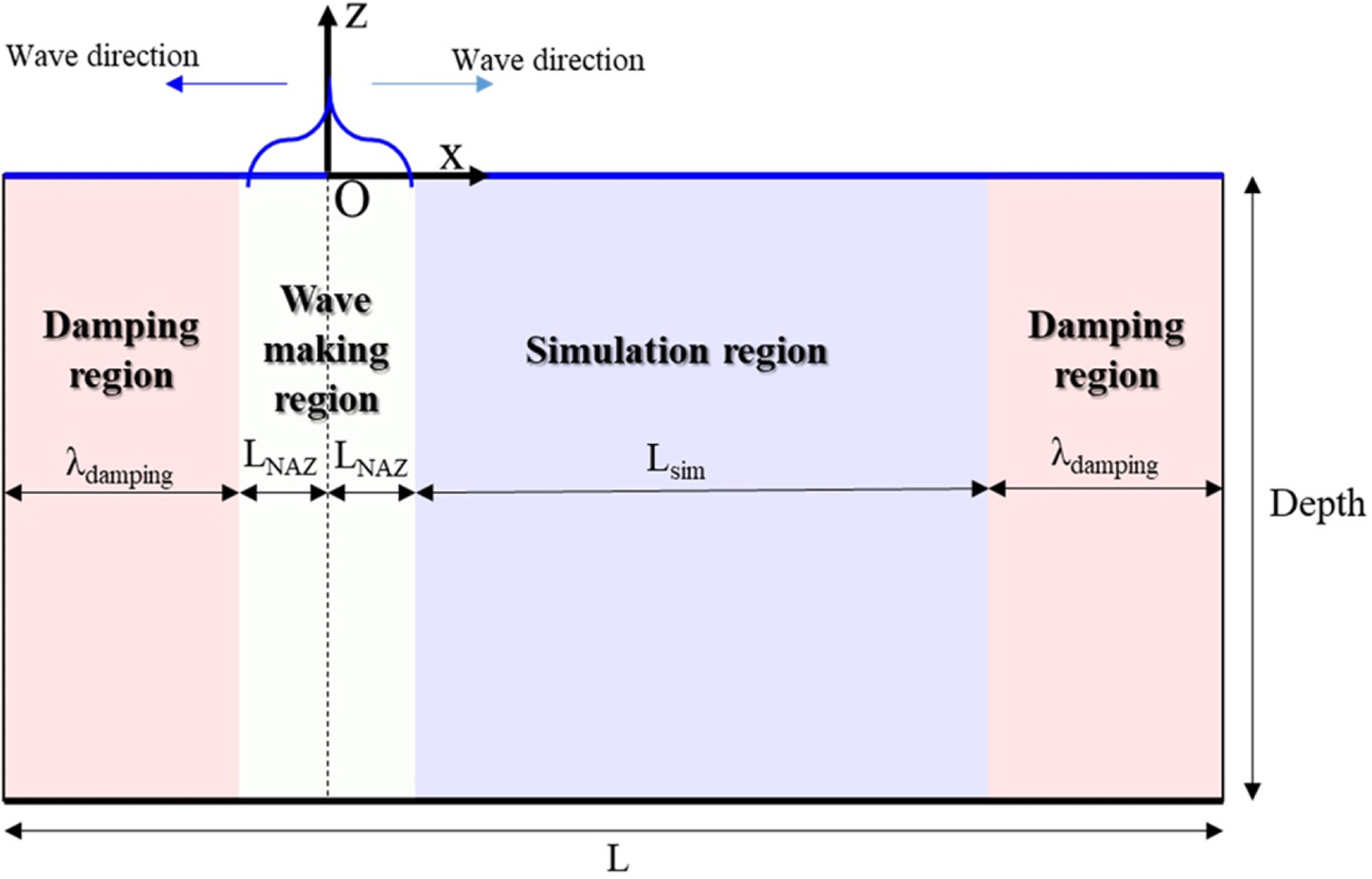
Because boundary conditions are undefined except those of the free surface, the conventional HOS method has limitations in implementing the boundary conditions of the piston- or flap-type wave maker, such as a traditional wave tank. Tuning through repetitive calculations is required because wave generation owing to the forced disturbance of free surface can be represented in a transfer function under linear free surface conditions alone and cannot be represented under nonlinear free surface conditions. Therefore, Kim (1993) applied the wave generation technique based on the submerged circular cylinder by merging the HOS method and the boundary element method, whereas Bonnefoy et al. (2006) adopted the pseudo-spectral basis of the cosine function and the additional potential technique to include the boundary condition for the wave generation unlike in the conventional HOS method. In this study, the feasibility of nonlinear wave generation was investigated via the forced disturbance of free surface using the wave transfer function at specific wave generation points unlike in the studies conducted by Kim (1993) and Bonnefoy et al. (2006). As earlier mentioned, the wave transfer function via the forced disturbance of free surface is only feasible under linear free surface conditions. Therefore, to make the wave transfer function possible in the nonlinear free surface, the nonlinear adjustment zone applied to the analytic and variational Boussinesq models by Liam et al. (2014) was introduced to the HOS method, as illustrated in Fig. 6. To prevent the inflow of waves owing to the periodic conditions at both ends, a damping zone was also applied, as illustrated in Fig. 6.

The nonlinear adjustment zone plays a role similar to the aforementioned adjustment scheme presented by Dommermuth (2000). The nonlinear term of the free surface boundary condition degrades the simulation stability of wave generation for wave disturbances at a specific wave generation point. Therefore, similar to scheme of Dommermuth (2000), which weakens the effect of nonlinear terms against time, it is necessary to mitigate the effect of nonlinearity on spaces. The study on the nonlinear adjustment zone in Section 3.2 was conducted by Liam et al. (2014) and it was inferred that a larger adjustment interval L_NAZ was required as the wave steepness increased.

The nonlinear adjustment zone is defined as a function of distance, as expressed in Eq. (26). The damping zone was applied to the boundary of both ends, as illustrated in Fig. 6. This was done to prevent the inflow and outflow of waves through the boundary owing to the periodic boundary conditions at both ends. The damping zone was applied to the physical quantity of each boundary condition, as expressed in Eq. (27).

where, x_a and x_b, γ_damping, and λ_damping denote the boundary points of the damping zone, wave damping coefficient, and length of the damping zone, respectively. In this study, γ_damping was set to one and λ_damping was set at a wavelength longer than the generated wavelength. If the nonlinear adjustment and damping zones are applied to the free surface boundary condition of Eqs. (3)–(4), they are defined as expressed in Eqs. (28)–(29).

Wave disturbances for wave generation were performed at the point where x was equal to zero, and the wave transfer function was calculated using the harmonic simulation results of white noise under the boundary condition of the linear free surface, as illustrated in Fig. 6.

4.2 Wave Generation Numerical Simulation

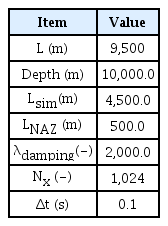
The wave generation simulation of regular and irregular waves was performed to verify and analyze the characteristics of the numerical technique for wave generation earlier described. The analysis was performed in the same calculation domain as in Fig. 7 under the calculation conditions presented in Table 4.

A wave transfer function can be created via the harmonic simulation results of white noise for the corresponding conditions, as illustrated in Fig. 8. ζ_influx denotes the disturbance amplitude of the wave at the point where x = 0.

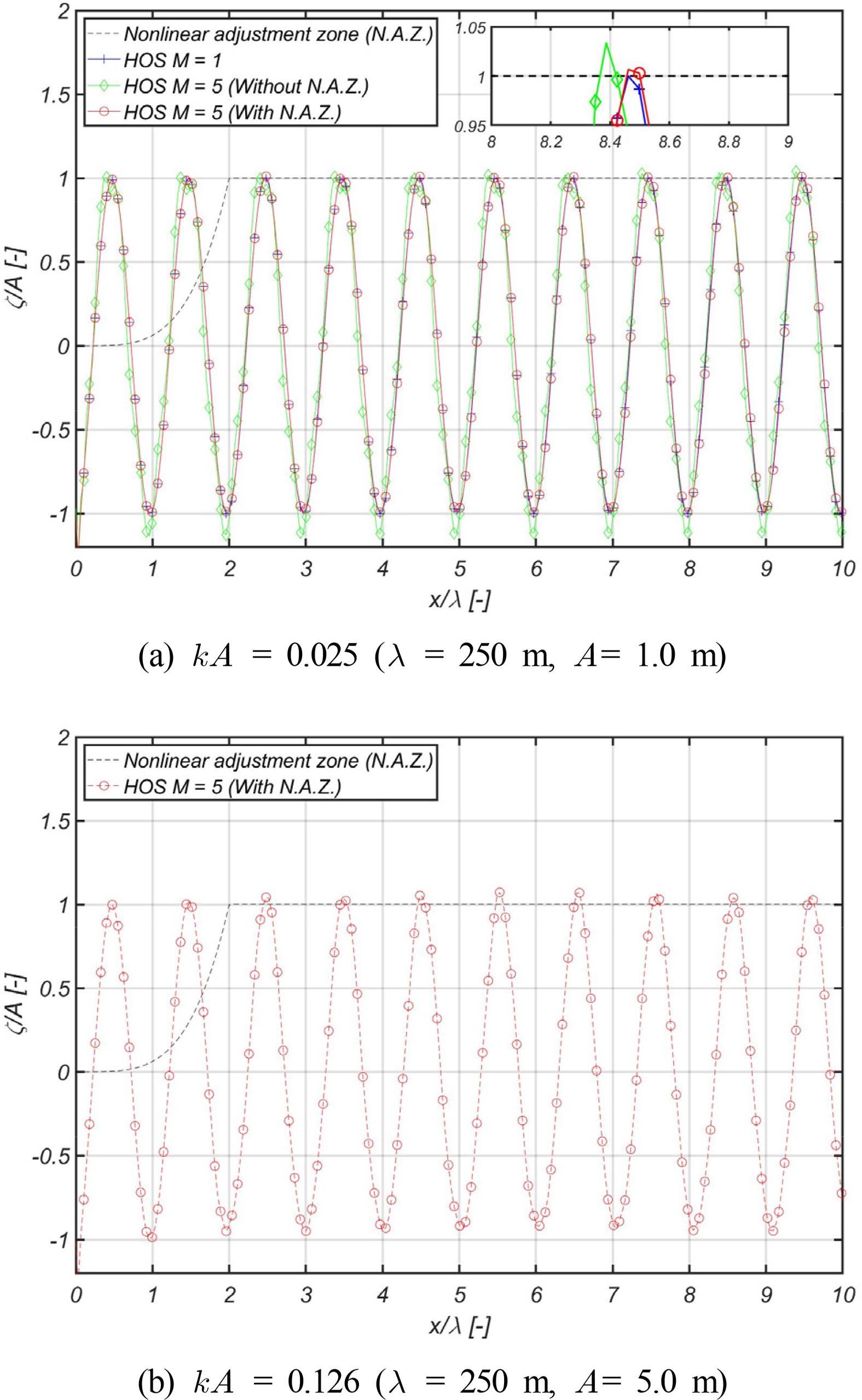
The wave generation simulation of regular waves was performed under the conditions of wave steepness, where k A was 0.025 and 0.126. The simulation that did not apply the nonlinear adjustment zone was additionally performed to understand the characteristics of the technique.

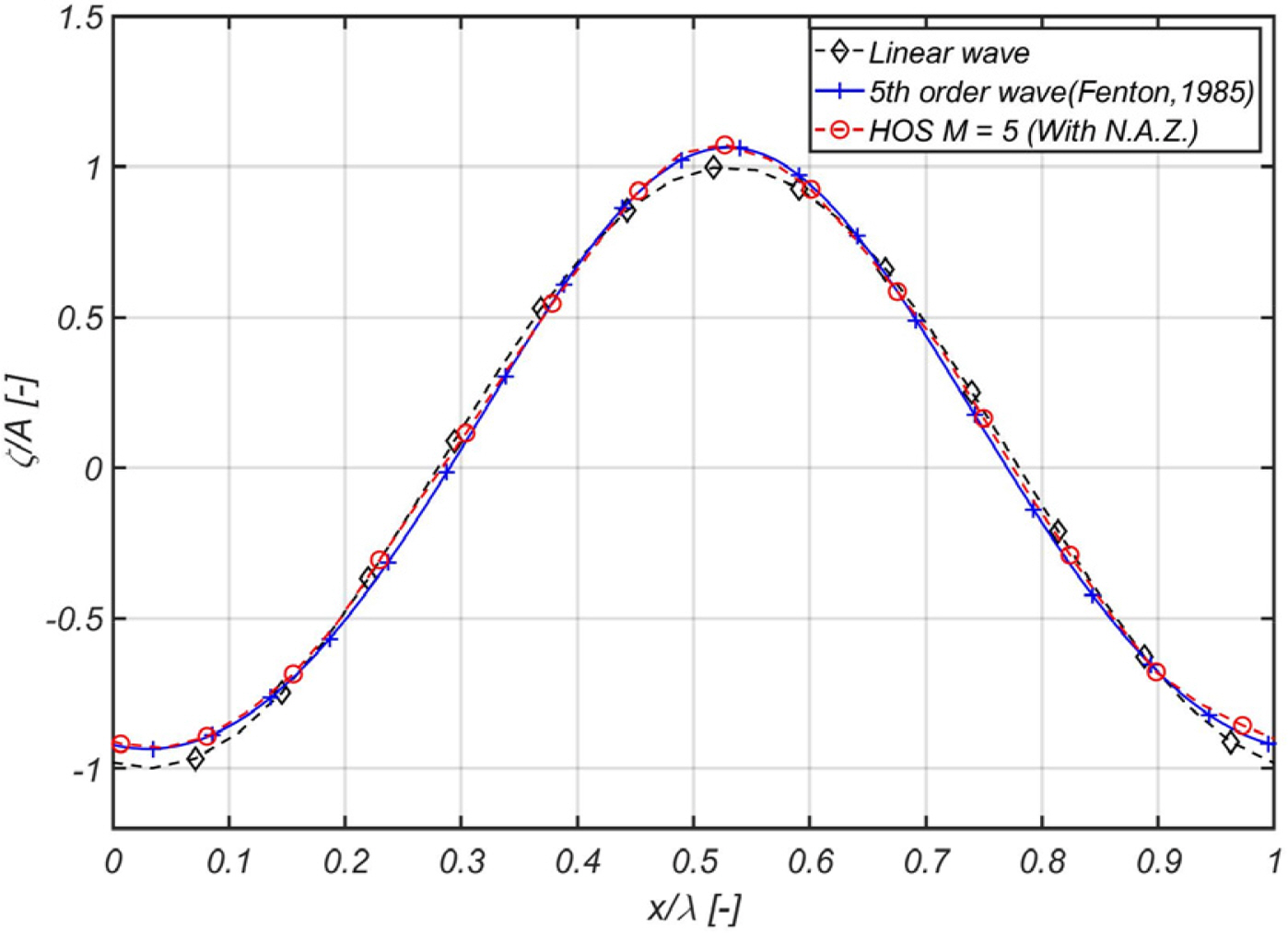
It was deduced that when kA is 0.025, it indicates the condition for generating waves with weak nonlinearity, where the amplitude difference between orders 1 and 5 is insignificant, as demonstrated in Fig. 9(a). In contrast, the condition when kA is 0.126 indicates the generation of waves with strong relative nonlinearity, which shows nonlinear characteristics with a high crest and steady trough, as demonstrated in Fig. 9(b). To strictly observe these nonlinear characteristics, it was compared with the 5th order Stokes wave (Fenton, 1985), as illustrated in Fig. 10. It was inferred that the shape of the generated wave did not only agree well with the 5th order Stokes wave, but also the waves of desired periods and amplitudes can be generated via the wave transfer function determined in advance, as demonstrates in Fig. 8. Regarding the application of nonlinear free surface boundary conditions without the nonlinear adjustment zone, the amplitude and phase of the wave differed from the linear result when kA was 0.025, and the simulation of regular wave generation diverged when kA was 0.126, as illustrated in Fig. 9(a). Consequently, it was concluded that it is necessary to apply a nonlinear adjustment zone when simulating wave generation via wave disturbance. It was determined that the HOS-based numerical harmonic tank can be implemented using a numerical technique such as nonlinear adjustment and damping zones based on the above results.

In the same calculation condition as the regular wave, the simulation of the irregular wave was performed for the irregular wave condition in Table 5. To observe the nonlinear effect according to the increase in the significant wave height, the simulation was performed under the three conditions of the mean wave steepness ( smean=kpHs/(22)), which are 0.01, 0.05, and 0.1. The simulation of wave generation was performed by also varying orders 1, 3 and 5.

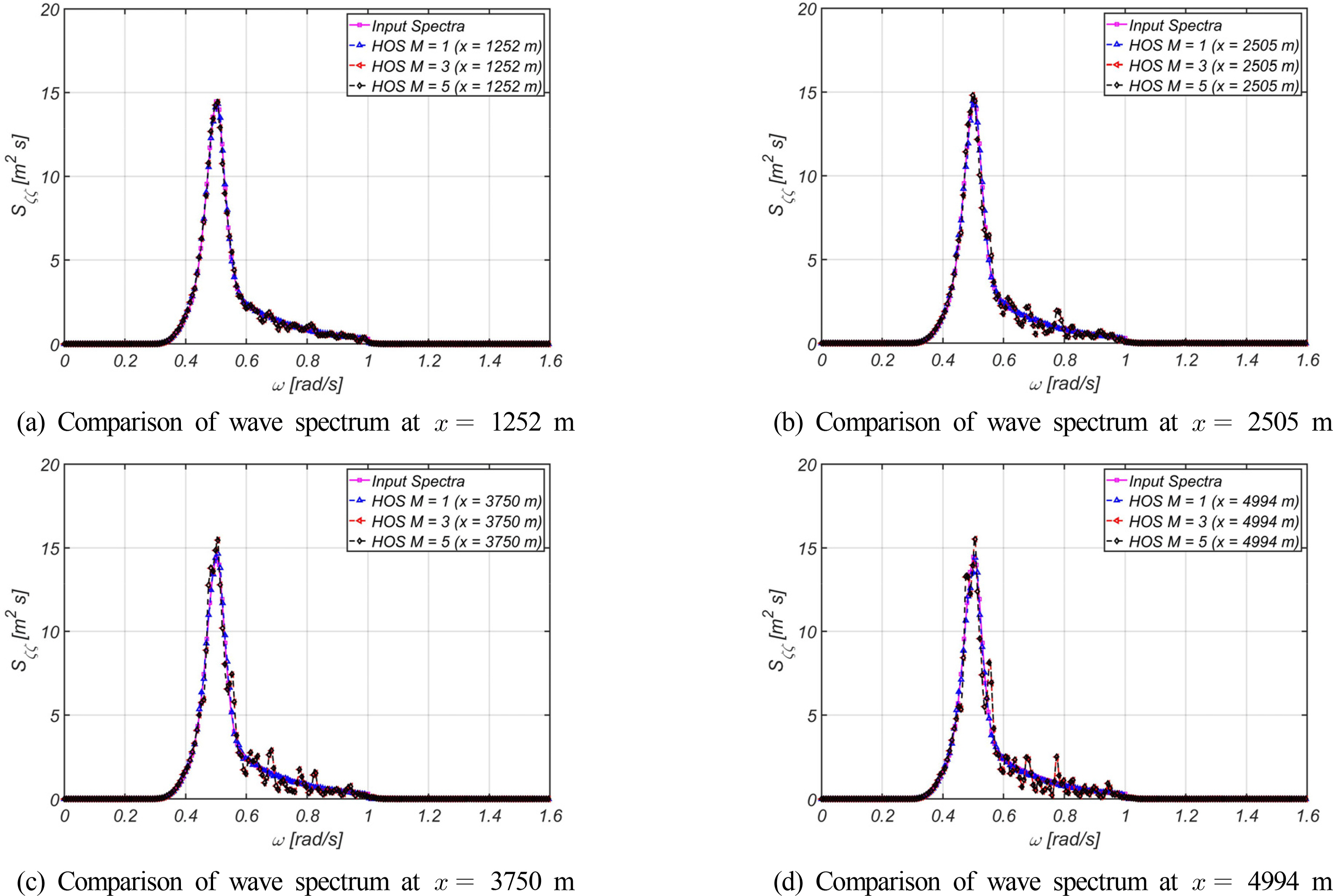
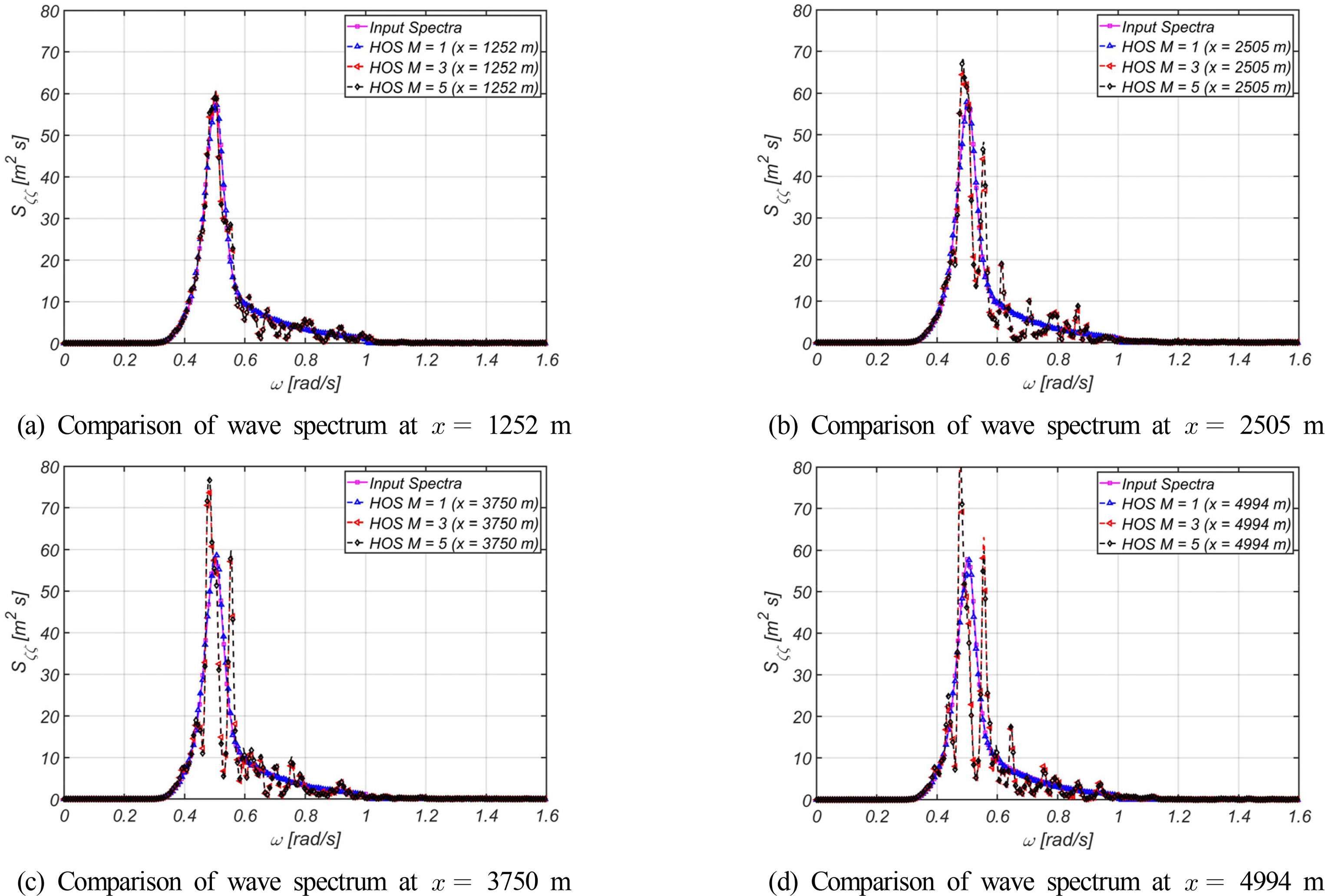
For comparison, the random phase was used identically in all simulations when generating irregular waves. After the relaxation distance of the nonlinear adjustment zone, a spectral analysis was performed on the wave time series at 4 points (x = 1252 m, 2505 m, 3750 m, and 4994 m).

Fig. 11 illustrates the mean wave steepness of 0.01. It was determined that the spectrum of 4 points almost coincide with no difference depending on the HOS order, and also that the spectrum of 4 points almost coincide with the spectrum input when generating the wave. It can be inferred that energy was not redistributed between frequencies because there was an insignificant nonlinear interaction between wave components during the generation and propagation of irregular waves. This means that the nonlinearity that appeared was insignificant owing to the low mean wave steepness of the calculation condition. Fig. 12 illustrates the mean wave steepness of 0.05. Except for the case of order 1, it was determined that the difference in the input wave spectrum increased with an increase in the distance from the origin, which is the wave generation point. This indicates that the energy distribution between frequencies was insignificant owing to the nonlinear interaction between wave components during wave propagation as earlier mentioned. Because the results of orders 3 and 5 are almost identical, it can be inferred that nonlinear interactions can also be reflected at order 3 when the mean wave steepness is 0.05. Fig. 13 presents the results of mean wave steepness at 0.1. It’s similarity to the input wave spectrum was apparent when x was equal to 1252 m, which is the closest point after the relaxation distance of the nonlinear adjustment zone during wave generation; however, the difference in the input wave spectrum increased as the wave propagated away from the origin of wave generation. Consequently, it can be inferred that the nonlinear interaction of the wave increased compared to the previously described wave steepness condition. Based on the comparison with the mean wave steepness of 0.05, it was deduced that the energy redistribution between wave components was more significant owing to the nonlinear interaction between wave components during wave propagation. Some differences between the results of orders 3 and 5 were determined, thus indicating that for the mean wave steepness of 0.1, nonlinear interactions can be fully reflected only when the order is considered to be 5 or above similar to the results of the irregular wave simulation in Section 3.2.