Lyapunov 재설계 방법을 이용한 무인 수상정의 군집 제어
Formation Control for Unmanned Surface Vessels Using Lyapunov Redesign Method
Article information
Trans Abstract
In this paper, a practical controller for a group of USVs is proposed in order to avoid matrix inversion problems in computation. Using nonlinear mapping, a formation composed of nonholonomic agents can be stabilized even when the formation is stationary. Since there is no matrix inversion in computing the control law, the computation complexity can be resolved. A controller for stabilizing the formation errors in the presence of model uncertainty is considered using the Lyapunov redesign method. The asymptotic stability of the formation errors is shown. It is also shown that the proposed controller can be applied to guide a formation to a different shape without modification.
1. 서 론
하나의 개체로 이루어진 무인 시스템이 가지는 물리적 한계를 극복하기 위하여 여러 대의 개체를 이용하는 시도가 오래전부터 이루어져왔다. 적용되는 공간에 따라 육상에서는 무인자동차(Unmanned ground vehicles, UGV), 공중에서는 무인비행기(Unmanned aerial vehicles, UAV), 그리고 최근에는 수상의 무인 수상정(Unmanned surface vehicles, USV) 및 무인 잠수정 (Unmanned underwater vehicles, UUV)등의 형태로 진행되어 왔다. 이중 USV 및 UUV 분야는 다른 분야에 비해 상대적으로 발전이 뒤처졌으나, 미 해군이 2007년 공식적으로 마스터플랜을 발간한 이후로는 활발한 연구가 이루어져왔다(US Navy, 2007). 특히 USV는 해수면 아래에 전개된 UUV 및 해수면 위쪽의 UAV등과 같은 다른 다중 무인시스템들과 협업하여 통신망 또는 감시를 위한 네트워크를 구성할 수 있어 많은 관심을 받고 있다. 이는 수면을 중심으로 상부의 대기권 내에 위치하는 시스템과 하부에 있는 수중 시스템이 서로 직접적인 통신을 하는 것이 어렵기 때문이다. 따라서 USV 시스템은 이러한 두 시스템 간에 접점으로서의 역할을 수행할 수 있으며 무인잠수정의 위치 추정에 이용할 수도 있다(Lim et al., 2005).
여러 대의 개체로 이루어진 시스템이 협업을 통하여 주어진 미션을 수행하기 위해서는 대형을 형성하여야 한다. 해양에서 이러한 대형의 형성 및 유지라는 주제는 오래 전부터 중요하게 다루어 졌다. 과거에는 여러 대의 전함들이 해 전을 치르는 동안 각각의 전함들의 움직임이 전술적 측면에서 제어가 이루어 졌고, 현대에도 상선들이 호위함들의 보호를 받으며 이동한다 던지, 대형 해양구조물을 해당 해역에 설치하기 위한 작업선들 간의 협업 등에도 군집에 대한 대형의 형성과 위치 제어라는 측면에서 바라볼 수 있다. 또한 여러 대의 수상정 또는 잠수정으로 이루어진 시스템의 경우 해양조사나 항만 방어 또는 해저면의 Subsea 시스템에 대한 검사 분야로의 응용이 시도되고 있다(Makrinos, 2004; Xiang et al., 2010). 이러한 해양시스템에서의 군집 제어에 대한 활용 예가 증가하면서 자율형 시스템의 대형 제어에 대한 알고리즘 연구도 점차 확대되고 있다 (Arrichiello et al., 2006, Breivik et al., 2008).
여러 대의 자율형 개체가 모여 하나의 대형을 생성하는 데 있어 가장 중요한 문제가 각각의 개체로 하여금 목표로 하는 대형을 형성할 수 있는 위치로 이동하도록 유도하고, 대형을 유지하도록 제어할 수 있는 규칙을 수립하는 것이다. 이러한 유도 및 제어에 관한 규칙을 수립하기 위해서는 각 개체에 대한 기준 위치가 주어져야 한다. 우선, 각 개체에 대해 기준 위치를 미리 설정하여 운용하는 방법을 고려할 수 있으나, 전체 시스템에 주어진 미션이 변하는 경우 대형의 움직임과 모양도 함께 변하기 때문에, 실시간 운영이 필요한 경우에는 적합하지 않다. 이에 따라 변화하는 미션에 대응하기 위해 실시간으로 기준 위치를 설정하는 방법으로 크게 Leader-follower(LF) 방법이나 Virtual structure(VS)를 이용하는 방법 등이 있다. LF 방법은 대형을 구성하는 전체 개체들 중 하나 또는 여러 개의 개체를 Leader로 설정하여 나머지 개체들을 지칭하는 Follower들의 위치를 Leader와의 상대적인 기하학적 관계를 이용하는 것이며, 대형 형성에 관한 부분에서 널리 사용되고 있다(Desai et al., 2001; Das et al. 2002). 하지만, 전체 대형의 움직임과 안정성이 Leader의 물리적 특성에 크게 의존한다는 단점이 있다. 이에 반해, Virtual structure를 이용하는 방법은 기준점을 모든 개체의 평균을 사용하여 설정하거나, 대형에서 가상의 중심 또는 Virtual structure의 중심에 고정하는 것이다(Lewis and Tan, 1997; Balch and Arkin 1998, Sadowska el al., 2011). VS 방법의 장점으로는 대형 내에서 모든 개체가 하나의 단일 개체로 취급되기 때문에 대형을 관리하는 것이 비교적 쉽다는 것이다. 하지만 전체 대형 내에서 각각의 개체가 가지는 물리적 제약이 명확하게 표시되기 어렵다는 단점이 있다. 따라서 Virtual structure를 통해 가상 기준을 사용하는 방법은 각각의 개체에 대한 제어 범위를 만족시키는 것이 매우 어려우며, 개체를 추가하거나 제거해야할 필요가 있을 때 대형 규모에 대한 확장성에도 문제가 발생할 수 있다.
기준 위치가 설정된 이후에는 이 위치로 개체들을 이동시키기 위한 유도 및 제어 법칙이 적용되어야 한다. 이는 목표 위치와 실제 위치와의 차이를 오차로 설정하여 이를 제거하기 위한 노력으로 정의할 수 있다. 전체 시스템에 대한 모델링을 수립하고 제어기를 구성할 때, 역행렬의 연산이 있을 수 있으며 행렬식이 0에 가까워질 때 문제가 발생할 수 있다. 이러한 문제를 해소하기 위하여 좌표계를 변경하여 행렬의 특성을 조절하는 방법을 도입할 수 있으며 좌표계 변경에 따른 비선형성이 강해진 시스템에 대해 비선형 제어 기법의 도입이 필요하다. 특히 모델링 오차가 많이 발생할 수 있는 해양시스템의 특성을 반영하기 위하여 불확실한 항이 존재하는 시스템에 대해 안정성을 담보할 수 있어야 하는데, 이러한 용도로 Lyapunov redesign법이 적용될 수 있다(Khalil, 2002).
본 논문에서는 유니사이클로 모델링되는 USV 또는 UUV들이 대형을 형성할 때, Leader-follower 방법과 Virtual structure를 이용하는 방법을 결합하여 VS내에서 기하학적 관계를 이용하여 대형을 생성 하고 기준 위치를 유지하는 방법을 제시하였다. 시스템 모델링을 바탕으로 제어 법칙을 수립할 때, 역행렬 을 연산하면서 발생할 수 있는 문제점을 해결하고, 불확실성을 포함하고 있는 비선형시스템에 대하여 대형 형성에 필요한 강인한 안정성을 갖는 제어기를 설계하기 위하여 Lyapunov redesign법을 적용하였다. 설계된 제어기가 초기 위치에서 목표로 하는 대형으로 이동하는 대형 생성뿐만 아니라, 원하는 대형의 형태가 바뀌어 새로운 대형으로의 유도가 필요할 때에도 오차를 효과적으로 제거할 수 있도록 구성하였으며, 주어진 시스템이 전역적으로 또한 안정적으로 목표 대형으로 유도 되는 것을 시뮬레이션으로 확인하였다.
2. 목표 대형의 생성 및 제어기 설계
2.1 대형의 생성 및 오차에 대한 정의
여러 개의 개체가 목표로 하는 하나의 대형을 형성하는 데 있어 각 개체들의 이상적인 위치와 실제 위치의 차를 오차로 정의할 수 있다. 이상적인 위치는 대형 내에서 각 개체간의 상호관계로 표현되는데, n개의 개체로 구성된 대형에 대하여 그 형상을 상호간의 관계로 특정하기 위한 조건을 대형 제약조건(Formation constraint)이라고 한다. R2에서 이러한 제약조건으로 다음과 같이 표현하는 방법을 고려할 수 있다.
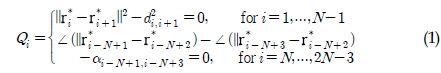
여기서 di,j는 i번째 개체와 j번째 개체의 이상적인 거리,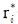 는 i번 째 개체의 목표 위치, αa,a+2는 두 벡터
는 i번 째 개체의 목표 위치, αa,a+2는 두 벡터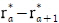 와
와  가 이루어야 할 이상적인 각도를 의미한다. 이와 같이 정의할 때 총 2N-3개의 제약조건들이 구성되고 이에 해당하는 대형은 하나이므로 Fig. 1에 나타나는 바와 같이 대형의 형태를 반영하는 데는 충분하다.
가 이루어야 할 이상적인 각도를 의미한다. 이와 같이 정의할 때 총 2N-3개의 제약조건들이 구성되고 이에 해당하는 대형은 하나이므로 Fig. 1에 나타나는 바와 같이 대형의 형태를 반영하는 데는 충분하다.
하지만 개체들의 연결이 순차적으로 이루어지기 때문에 k - 1번째 제약조건 Qk-1과 k번째 제약조건 Qk가 서로 의존적이며, 이러한 형태의 대형은 개체가 추가되는 경우 확장된 형태로 표현하는 것이 어렵다. 대형을 정의하는 다른 방법으로는 (Egerstedt and Hu, 2001)이 제안한 바와 같이 제약 조건을 하나의 함수로 표현할 수 있지만 이럴 경우 대형에 대한 정의가 개체의 숫자에 종속된다. 따라서 제약조건을 만족시키는 대형이 단 하나이면서도 제약조건의 수가 개체의 수 n의 배수 형태로 표현되는 방법이 필요한 데 이를 위해 가상 리더(Virtual leader, VL)의 개념을 도입할 수 있다. 이를 통해 대형을 구성하는 제약 조건들이 서로 독립적이면서, 대형을 형성하는 개체가 추가될 때에도 자연적인 확장이 가능해진다. 가상 리더를 도입하여 얻을 수 있는 또 다른 이점으로는 특정한 강체 대형의 움직임이 가상 리더들에 의해 유도될 수 있다는 점이다. 두 개의 가상 리더 VL1과 VL2에 대하여 각각의 위치 벡터를 ru1 과 ru2라고 할 때, 제약 조건들은 다음과 같이 표현될 수 있다.
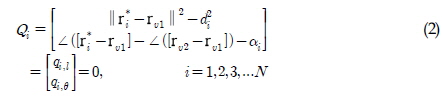
이러한 대형 제약 조건들에 대한 표현법은 위에서 언급한 조건들을 만족시킬 수 있으며, 이 조건들을 이용하여 오차에 대한 정의를 도출할 수 있다. 대형을 정의하는 제약조건에서의 오차는 식 (3)와 같이 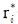 를 ri로 바꿈으로서 표현할 수 있다.
를 ri로 바꿈으로서 표현할 수 있다.

즉, 각 개체가 위치해야 할 이상적인 위치를 가상 리더들과의 거리 및 각도 정보를 이용하여 정의하는 것이다. 이에 따라 오차값은 각 개체들이 가상리더 중 하나와의 거리 및 가상 리더들과 이루는 각도가 이상적인 거리 및 각도의 값가 차이가 나는 정도를 나타내게 된다.
2.2 대형의 생성을 위한 모델링 및 제어기 설계
R3 공간상에서 개체들에 대해 대형 생성 시 발생하는 오차를 안정화시키기 위한 제어기를 설계하기 위하여 우선 기구학적 모델을 다음과 같이 표현하도록 한다.

N개의 개체로 이루어진 대형에서 zi 는 i번째 개체의 상태벡터를 나타내고, ui 는 제어 입력을 표시하며, ri는 관성좌표계에 대한 개체의 위치를 표현하는 벡터이다. 오차에 대해서는 다음과 같이 벡터 형식으로 나타낼 수 있다.

따라서 오차에 대한 동역학 식은 아래와 같이 표현되며,
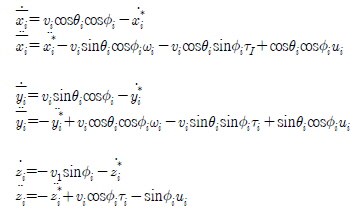
다음과 같이 정리하여 표현할 수 있다.

여기서
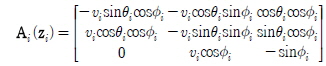
이고, 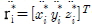 이다.
이다.
식 (6)에서 vi 가 다음의 조건을 만족한다고 가정하면,
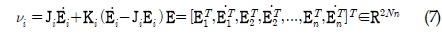
Lyapunov 함수는 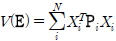 의 형태로 표현될 수 있다.
의 형태로 표현될 수 있다.
여기서 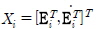 이고 Pi 는 R2n × 2n 에서 Symmetric positive definite 행렬이다. 식 (6)와 식 (7)에 대해, Xi 는 다음의 조건을 만족시켜야 한다.
이고 Pi 는 R2n × 2n 에서 Symmetric positive definite 행렬이다. 식 (6)와 식 (7)에 대해, Xi 는 다음의 조건을 만족시켜야 한다.
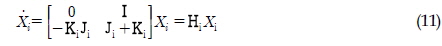
안정도를 판별하기 위한 Lyapunov 함수의 미분은  로 나타난다.
로 나타난다. 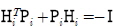 을 만족시키는 Pi 에 대해
을 만족시키는 Pi 에 대해 가 성립하며 주어진 Lyapunov 함수에 대해 다음의 부등식들이 성립하게 된다.
가 성립하며 주어진 Lyapunov 함수에 대해 다음의 부등식들이 성립하게 된다.
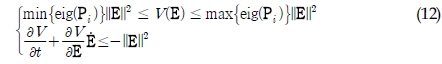
따라서, 대형 생성 시 발생하는 오차에 대해 시스템이 지수적으로 그리고 전역적으로 안정화 될 수 있다(Khalil, 2002). 위 결과를 바탕으로 하여 대형을 구성하는 데 필요한 제어기 ui 는 다음과 같이 설계할 수 있다.

3. 특이점을 고려한 제어기의 설계
3.1 특이점의 성질
앞서 설명한 제어기의 경우 ui =0 일 때 역행렬이 존재하지 않아 문제가 발생할 수 있으며, ui ≠0 이라고 하더라도, 역행렬을 계산할 때 ui < ε 에 대해 ill-conditioned가 되는 작은 값 ε이 존재한다. 따라서 개체들이 목표 지점에 접근하여 오차 값이 작아짐에 따라 연산에서 문제가 발생할 가능성이 커지게 된다. 이러한 문제를 해결하기 위해 직교좌표계에서 개체를 나타내는데 사용한 유니사이클 모델에 대해 안정화 문제를 고려해야 하는데, 일반적으로는 안정화 되기 어려운 것으로 알려져 있다(Brockett, 1983). 이러한 문제를 해결하기 위해 비선형 좌표변환을 이용하여 안정화를 시도할 수 있다(de Wit and Sørdalen, 1992). 직교좌표계에서 극좌표계로의 변환은 그러한 비선형 좌표 변환의 한 예이다. 극좌표계에서 유니사이클을 표시하는 방법은 (Astolfi, 1999; Badreddin and Mansour, 1993)에서 다룬바 있다. 극좌표와 직교좌표계에서의 표현에 관한 상관관계는 Fig. 2에 나타내었다.
극좌표계에서의 유니사이클 모델은 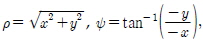 그리고 σ = ψ − θ라고 할 때, 식 (14)과 같이 표현할 수 있다.
그리고 σ = ψ − θ라고 할 때, 식 (14)과 같이 표현할 수 있다.

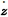 = f(z,u) 로 나타낼 수 있으며, z는 상태 벡터이고, u는 제어 입력을 나타내는 벡터이며, 함수 f의 정의역은 D=R2−{0}이다. 원점에서의 안정성을 조사하기 위하여 D 에서 Lyapunov 함수 Vp를 다음과 같이 정의하도록 하자.
= f(z,u) 로 나타낼 수 있으며, z는 상태 벡터이고, u는 제어 입력을 나타내는 벡터이며, 함수 f의 정의역은 D=R2−{0}이다. 원점에서의 안정성을 조사하기 위하여 D 에서 Lyapunov 함수 Vp를 다음과 같이 정의하도록 하자.
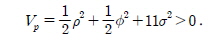
Lyapunov 함수 Vp 를 식 (14)에 나타난 경로를 따라 미분을 하면 다음과 같다.

M, k1 , k2 를 양의 상수라고 할 때, 제어 입력 u와 w를 다음과 같이 설정한다.
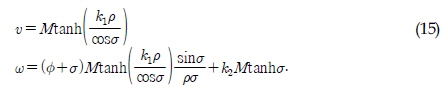
x∈R에 대해 0 < 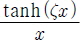 ≤ ζ 가 성립하므로, Vp의 도함수는 D 에서 다음과 같이 항상 Negative definite이다.
≤ ζ 가 성립하므로, Vp의 도함수는 D 에서 다음과 같이 항상 Negative definite이다.

이 제어기를 식 (6)에 나타난 제어기에 적용하기 위하여 속도를 시간에 대해 미분하면 다음과 같다.

따라서 |ui|< ε에 대해 i번째 개체를 위한 제어입력은 다음과 같은 형태로 정리할 수 있다.

3.2 Lyapunov redesign법을 이용한 제어기 설계
각각의 개체에 대해 동역학적인 해석을 수행할 때 시스템 모델링에 불확실한 요소들이 있다면 공칭 플랜트를 위해 설계된 제어기는 대형의 안정성을 담보할 수 없다. i번째 개체를 위한 모델링에 불확실성을 포함하도록 하기 위해 다음의 식으로 나타난다고 하자.
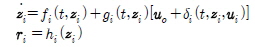
일반적으로 fi 와 gi 는 알려진 함수를 사용할 수 있는 반면 δi는 파라미터의 불확실성, 모델의 단순화 등과 같은 오차들을 포함하며 명확하게 정의되지는 않는다. 공칭 플랜트를 위해 정확하게 설계된 제어기를 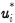 라고 하면, 이 제어 입력은 대형 오차에 대하여 지수적으로 안정화시킨다고 할 수 있으므로, i번째 개체에 대해 Lyapunov 함수 Vi(Ei) =
라고 하면, 이 제어 입력은 대형 오차에 대하여 지수적으로 안정화시킨다고 할 수 있으므로, i번째 개체에 대해 Lyapunov 함수 Vi(Ei) =  는 다음의 조건을 충족시키게 된다.
는 다음의 조건을 충족시키게 된다.
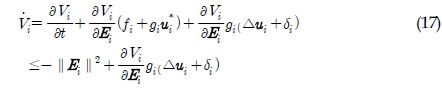
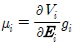 로 두고, 마지막 부등호 부분을 다시 정리하면,
로 두고, 마지막 부등호 부분을 다시 정리하면,

와 같이 나타난다. 여기서 시스템에 대한 불확실성을 나타내는 δi 가 다음 조건을 만족한다고 가정하자.
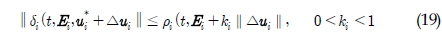
식 (18)의 우변 항에서 식(19)의 가정을 적용하여 다음의 부등 식을 유도할 수 있다.
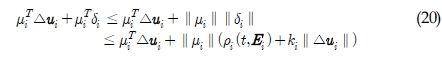
Δui에 대하여 다음의 형태를 취하면

식 (18)에 나타난 부등식의 우변항은 다음과 같이 정리된다.
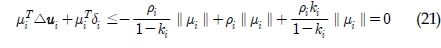
따라서 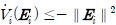 이 성립한다. 따라서 i번째 개체에 대해 제어기를 다음과 같이 설정할 경우 δi의 불확실성을 가지고 있는 시스템을 안정화 시킬 수 있게 된다.
이 성립한다. 따라서 i번째 개체에 대해 제어기를 다음과 같이 설정할 경우 δi의 불확실성을 가지고 있는 시스템을 안정화 시킬 수 있게 된다.

3.3 대형 형성 유도
앞에서 제시된 제어기는 모든 개체들이 각각의 개체들 간에 정의된 거리를 유지하는 문제 즉 이상적 위치와 실제 위치의 오차를 최소화 하는 데 초점이 맞춰져 있고, 원하는 대형의 유도에 대해서는 명확히 제시하지 못하는 단점이 있다. 여러 개의 개체들을 공통으로 주어진 미션을 수행하도록 운영하기 위해서는 생성된 대형을 유도하기 위한 법칙이 필요하다. 앞서 설계된 제어기를 사용하여 강체 대형을 생성시키기 위해 가상의 리더들을 도입하였다. 이러한 가상의 개체들은 대형을 유도하는 법칙으로 확장하는 데도 사용될 수 있다. 강체 대형은 R2 에서 N개의 개체와 2개의 가상 개체로 구성된 Virtual structure(VS )로 가정된다. 가상 개체를 제어하여 선형 속도 UVS 와 각가속도 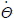 로 움직이는 강체 대형을 구성하기 위해서는 속도, 각가속도 그리고 강체 대형 사이의 관계를 구하여야 한다. 국부 좌표계 B가 VS 에 고정되어 있고, 그 원점을 OB 로 가정한다. ru1, ru2, 그리고 rVS 를 첫 번째 가상 개체, 두 번째 가상 개체, 그리고 좌표계 B의 관성 좌표계에 대한 위치벡터로 표기한다. 관성 좌표계상의 값에 대해 좌표계 I 를 사용할 때, 위치 벡터의 좌표는 다음과 같이 표현할 수 있다.
로 움직이는 강체 대형을 구성하기 위해서는 속도, 각가속도 그리고 강체 대형 사이의 관계를 구하여야 한다. 국부 좌표계 B가 VS 에 고정되어 있고, 그 원점을 OB 로 가정한다. ru1, ru2, 그리고 rVS 를 첫 번째 가상 개체, 두 번째 가상 개체, 그리고 좌표계 B의 관성 좌표계에 대한 위치벡터로 표기한다. 관성 좌표계상의 값에 대해 좌표계 I 를 사용할 때, 위치 벡터의 좌표는 다음과 같이 표현할 수 있다.
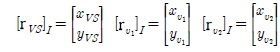
각각의 개체와 마찬가지로 VS 에 대해 유니사이클 모델을 적용할 경우 다음과 같이 나타난다.
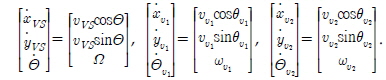
가상 개체의 위치는 다른 개체와 중복되지 않는 한 VS 상에서 자유롭게 선택할 수 있다. 한 개의 개체를 VS 의 중심에 위치시키는 이유는 모든 개체들이 비홀로노믹한 동역학을 지니고 있더라고 원점이 홀로노믹하게 움직일 수 있기 때문이다. 즉 비홀로노믹 개체들로 구성된 강체 대형이 홀로노믹한 동역학을 가지고 있는 개체의 궤적을 따라갈 수 있다는 것이다. 이러한 이점을 활용하기 위하여 첫 번째 가상 개체는 B 프레임의 원점에 설정이 되고, 두 번째 개체의 위치는 프레임 B 에 대해 위치벡터 dv2로 표현한다. 따라서, [dv2]B = [dv2,0]T로 나타낼 때 다음과 같이 나타난다.

속도에 관한 식은 식 (22)를 시간에 대해 미분하여 구하며, 다음과 같이 나타난다.

VS를 선속도 uVS= U및 각속도 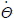 = Ω로 움직이게 하기 위해서는, 가상 리더들의 선속도 및 각속도인 uu1, uu2, wu1 그리고 wu2 값들이 U 와 Ω값에 따라 선정되어야 한다. 가상 리더들에 대한 제어입력 값들은 식 (24)을 사용하여 구할 수 있다.
= Ω로 움직이게 하기 위해서는, 가상 리더들의 선속도 및 각속도인 uu1, uu2, wu1 그리고 wu2 값들이 U 와 Ω값에 따라 선정되어야 한다. 가상 리더들에 대한 제어입력 값들은 식 (24)을 사용하여 구할 수 있다.
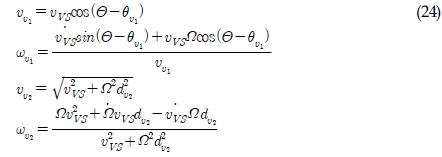
4. 시뮬레이션
4.1 강체 대형의 이동
설계된 제어기의 실효성을 검증하기 위하여 6개의 개체로 이루어진 시스템에 대해 삼각형 모양의 대형을 형성하여 이동하는 시뮬레이션을 수행하였다. 총 80초 동안 목표 지점까지 강체 대형을 유지하면서 기동하는 것으로 가정하였다. 관성좌표계를 중심으로 전체 대형의 회전이 없는 경우와 있는 경우 2가지로 구분하여 진행하였다. 우선 Fig. 3는 Ω=0일 때, 즉 관성좌표계에 대한 회전이 없이 6개의 개체로 구성된 삼각형 대형에서 각각의 개체가 이동하고 있는 경로를 보여준다. 최종 위치까지 이동하는 동안 시간이 16초, 32초, 48초, 64초 경과한 상태에서의 대형의 위치와 모양이 함께 나타나 있다. 그림에 나타난 바와 같이 목표 지점으로 움직이는 동안 개별 개체는 회전 및 병진 운동이 동시에 이루어지고 있지만, 전체 삼각형 형태의 대형은 회전이 없이 병진운동만으로 곡선형태의 경로를 따라 움직이고 있다는 것을 알 수 있다.
Fig. 4는 Ω=0.1 rad/sec 일 때, 즉 전체 대형이 시계방향으로 일정한 각속도로 회전하고 있을 때의 기동을 나타내고 있다. 앞선 예와 마찬가지로, 최종 위치까지 이동하는 동안 시간이 16초, 32초, 48초, 64초 경과한 상태에서의 대형의 위치와 모양이 함께 나타내었다. 가상리더에 대한 상대적인 거리와 각도를 유지하면서 동시에 전체 대형의 회전에 관한 제어가 이루어지고 있다. 그림 4와 5에 나타난 바와 같이 강체 대형의 방향은 경로의 곡률과는 무관하다. 이에 반해 일반적으로 Leader-follower 모델에 의해 생성된 대형의 경우 경로의 곡률에 영향을 받게 된다. 따라서, 제안된 대형제어의 유도 법칙을 이용하여 일반적인 Leader-follower 모델에서 보이는 거동의 단점을 Virtual structure 개념과 결합하여 보완하는 것이다.
4.2 대형의 전환을 위한 유도
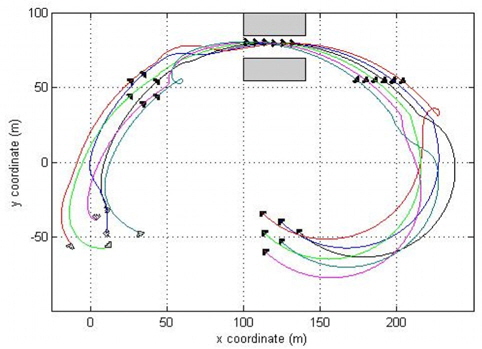
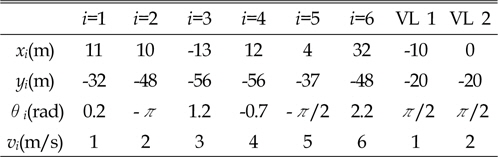
경우에 따라서는 대형의 모양이 변할 수도 있다. 즉 여러 대의 개체들이 모여 초기 대형을 형성하였다가 주어진 미션이 변경된 새로운 형태의 대형이 요구될 수도 있기 때문이다. 예를 들면 대형의 경로에 장애물이 존재하거나, 좁은 수로를 통과하는 경우 등이다. 이러한 요구에 대처하기 위하여 대형의 모양이 변하는 것을 대형 재생성이라고 한다. 앞서 설명한 바와 같이, 대형의 모양은 VS 에 설정된 국부좌표계 B에서 정의되는 개체들의 목표 지점으로 표현할 수 있다. 이에 따라, 대형의 형태가 변할 때, 국부좌표계 B에서 각 개체들의 위치가 다시 지정된다. 기존 대형에서 목표로 하는 대형의 모양이 변하여, 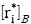 가 재설정될 때 목표 위치와 현재 위치의 차이, 즉, 오차가 크게 발생하게 된다. 대형의 모양이 재설정되어 변화하는 경우에도 별도의 유도 법칙을 사용하지 않고 앞서 설계된 제어기를 적용하는 시뮬레이션을 수행하였다. 초기조건을 표 1에 나타난 바와 같이 설정하였다.
가 재설정될 때 목표 위치와 현재 위치의 차이, 즉, 오차가 크게 발생하게 된다. 대형의 모양이 재설정되어 변화하는 경우에도 별도의 유도 법칙을 사용하지 않고 앞서 설계된 제어기를 적용하는 시뮬레이션을 수행하였다. 초기조건을 표 1에 나타난 바와 같이 설정하였다.
6개의 개체와 가상 리더 2개로 이루어진 시스템에 대해 위치, 방향 및 초기 속도에 대해 각각 다른 상황을 설정한 후 결과는 Fig. 5와 Fig. 6에 나타내었다.
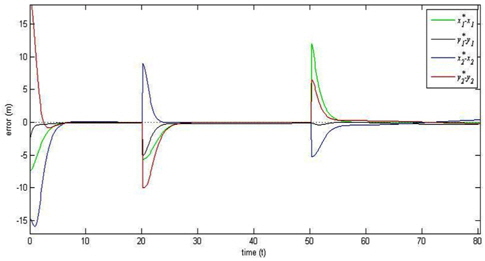
6개의 개체들이 먼저 6각형의 초기 대형을 구성하게 되고, 20초 경과 뒤 좁은 수로를 통과한다는 가정 하에 직선의 형태로 전환되도록 하였다. 수로를 빠져나온 개체들에 대하여 기동 시작 후 50초 되는 시점에 삼각형의 대형으로 변환되도록 하였다. 대형을 형성하는 6개의 개체들 중 첫 번째와 두 번째 개체에 대한 위치 오차 변화 추이를 Fig. 7에 나타내었다. 나머지 개체들에 대한 위치 오차 변화도 비슷하게 나타나므로 그림에는 생략하였다. 예상할 수 있듯이, 초기 대형 형성 시점, 20초 경과 시점, 그리고 50초 경과 시점에서 대형의 모양이 변화함에 따라 자연스럽게 대형 오차가 크게 발생하는 것을 볼 수 있다. 그림에 나타난 바와 같이 대형의 형태를 유지하는 데 사용된 제어기를 형태의 변화 없이 대형을 유도하는 데도 성공적으로 적용된다는 것을 알 수 있다. 이는 본 논문에서 제안된 제어기가 오차를 전역적으로 감소시킬 수 있으며, 이에 따라 대형을 유지하기 위한 제어 뿐만 아니라, 목표 대형으로의 유도에도 그대로 사용가능하다는 것을 의미한다.
5. 결론 및 향후 계획
본 논문에서는 무인 수상정 또는 무인 잠수정들이 대형을 형성하도록 하기위해 각 개체들에 대한 제어기를 설계하는 문제를 다루었다. 우선, 일반적인 시스템에서 제어 입력 값을 계산하기 위하여 역행렬을 계산할 때 발생할 수 있는 문제점을 해결하기 위하여 비선형좌표 변환을 수행하고, 개체 동역학에서 불확실한 항들에 대한 강인한 안정성을 확보하기 위하여 Lyapunov 재설계 방법을 적용하여 제어기를 설계하였다. 또한 Leader-follower법과 Virtual structure법을 혼합한 유도 기술을 제시하여 목표 대형이 요구되는 선속도와 각속도를 가지고 운동할 수 있도록 하였다. 마지막으로, 시뮬레이션을 통하여 대형이 강체의 형태로 경로를 따라가는 것 뿐 아니라, 대형의 모양이 변하여 유도가 필요한 경우에도 기존 대형 유지에 사용되는 제어기를 적용하여 원하는 결과를 얻을 수 있다는 것을 보였다.
제안된 제어기가 실제 해양환경에서 사용되기 위해서는 유체동역학적인 힘을 추가로 고려하여야 한다. 이는 환경하중에 의한 뿐만 아니라 대형의 형성, 유지 및 변환을 수행하기 위한 시스템의 모델링에 나타나는 여러 개체간의 관계에서 형성되는 연성 효과를 추가하는 것을 의미한다. 제안된 제어기의 활용성을 높이기 위하여, 관성항을 포함하는 동역학 모델을 수립하고 연성효과를 분석하는 작업이 추가로 진행될 것이다.
Acknowledgements
이 논문은 2013학년도 동의대학교 교내연구비에 의해 연구되었음(2013AA167)
References
Arrichiello, F., Chiaverini, S., Fossen, T.I., 2006. Formation Control of Underactuated Surface Vessels using the Null-Space-Based Behavioral Control, Proceeding of IEEE Int. Conf. on Intelligent Robots and Systems.
Arrichiello F., Chiaverini S., Fossen T.I.. Formation Control of Underactuated Surface Vessels using the Null-Space-Based Behavioral Control In : Proceeding of IEEE Int. Conf. on Intelligent Robots and Systems; 2006.Astolfi, A., 1999. Exponential Stabilization of a Wheeled Mobile Robot via Discontinuous Control. Journal of Dynamic Systems, Measurement, and Control, 121, 121-126.
Astolfi A. Exponential Stabilization of a Wheeled Mobile Robot via Discontinuous Control. Journal of Dynamic Systems, Measurement, and Control 1211999;:121–126. http://dx.doi.org/10.1115/1.2802429.Badreddin, E., Mansour, M., 1993. Fuzzy-tuned State Feedback Control of a Nonholonomic Mobile Robot. IFAC World Congress, Sydney Australia, 6, 577-580.
Badreddin E., Mansour M.. Fuzzy-tuned State Feedback Control of a Nonholonomic Mobile Robot In : IFAC World Congress. 61993. p. 577–580.Balch, T., Arkin, R.C., 1998. Behavior-Based Formation Control for Multirobot Teams. IEEE Transactions on Robotics and Automation, 14(6), 926-939.
Balch T., Arkin R.C.. Behavior-Based Formation Control for Multirobot Teams. IEEE Transactions on Robotics and Automation 14(6)1998;:926–939. http://dx.doi.org/10.1109/70.736776.Breivik, M., Hovstein, V.E., Fossen, T.I., 2008. Ship Formation Control: A Guided Leader-Follower Approach. Proceeding of IFAC World Congress, 16008-16014.
Breivik M., Hovstein V.E., Fossen T.I.. Ship Formation Control: A Guided Leader-Follower Approach In : Proceeding of IFAC World Congress; 2008. p. 16008–16014.Brockett, R.W., 1983. Asymptotic Stability and Feedback Stabilization. in Differential Geometric Control Theory. Birkhauser, Boston, Massachusetts, 181-191.
Brockett R.W.. Asymptotic Stability and Feedback Stabilization. in Differential Geometric Control Theory Birkhauser. Boston, Massachusetts: 1983. p. 181–191.Das, A.K., Fierro, R., Kumar, V., Ostrowski, J.P., Spletzer, J., Taylor, C.J., 2002. A Vision-Based Formation Control Framework. IEEE Transactions on Robotics and Automation. 18(5), 813-825.
Das A.K., Fierro R., Kumar V., Ostrowski J.P., Spletzer J., Taylor C.J. A Vision-Based Formation Control Framework. IEEE Transactions on Robotics and Automation 18(5)2002;:813–825. http://dx.doi.org/10.1109/TRA.2002.803463.Desai, J.P., Ostrowski, J.P., Kumar, V., 2001. Modeling and Control of Formations of Nonholonomic Mobile Robots. 17(6), 905-908.
Desai J.P., Ostrowski J.P., Kumar V.. Modeling and Control of Formations of Nonholonomic Mobile Robots. IEEE Transactions on Robotics and Automation 17(6)2001;:905–908. http://dx.doi.org/10.1109/70.976023.de Wit, C.C., Sørdalen, O.J., 1992. Exponential Stabilization of Mobile Robots with Nonholonomic Constraints. IEEE Transactions on Automatic Control, 37(11), 1791-1797.
de Wit C.C., Sørdalen O.J.. Exponential Stabilization of Mobile Robots with Nonholonomic Constraints. IEEE Transactions on Automatic Control 37(11)1992;:1791–1797. http://dx.doi.org/10.1109/9.173153.Egerstedt, M. and Hu, X., 2001. Formation Constrained Multi-Agent Control. IEEE Transactions on Robotics and Automation, 17(6), 947-951.
Egerstedt M., Hu X. Formation Constrained Multi-Agent Control. IEEE Transactions on Robotics and Automation 17(6)2001;:947–951. http://dx.doi.org/10.1109/70.976029.Khalil, H.K., 2002. Nonlinear Systems. 3rd Edition, Prentice Hall, Upper Saddle River, New Jersey.
Khalil H.K.. Nonlinear Systems Prentice Hall. Upper Saddle River, New Jersey: 2002. 3rd Editionth ed.Lewis, M.A., Tan, K.H., 1997. High Precision formation Control of Mobile Robots Using Virtual Structures. Autonomous Robots, 4(4), 387-403.
Lewis M.A., Tan K.H. High Precision formation Control of Mobile Robots Using Virtual Structures. Autonomous Robots 4(4)1997;:387–403. http://dx.doi.org/10.1023/A:1008814708459.Lim, J.H., Kang, C.U., Kim, S.K., 2005. A Study on a 3-D Localization of a AUV Based on a Mother Ship. Journalof Ocean Engineering and Technology, 19(2), 74-81.
Lim J.H., Kang C.U., Kim S.K.. A Study on a 3-D Localization of a AUV Based on a Mother Ship. Journalof Ocean Engineering and Technology 19(2)2005;:74–81.Makrinos, S.T., 2004. United States Port Security in the War on Terrorism. Sea Technology, 45(3), 33-34.
Makrinos S.T.. United States Port Security in the War on Terrorism. Sea Technology 45(3)2004;:33–34.US NAVY, 2007. The Navy Unmanned Surface Vehicle (USV) Master Plan. [Online] Available at: <http://www.navy.mil/navydata/technology/usvmppr.pdf> [Accessed 31 Dec. 2013].
The Navy Unmanned Surface Vehicle (USV) Master Plan 2007. http://www.navy.mil/navydata/technology/usvmppr.pdf.Sadowska, A., Broek, T.v.d., Huijberts, H., Wouw, N.v.d., Kostic, D., Nijmeijer, H., 2011. A virtual structure approach to formation control of unicyle mobile robots using mutual coupling. International Journal of Control, 84(11), 1886-1902.
Sadowska A., Broek T.v.d., Huijberts H., Wouw N.v.d., Kostic D., Nijmeijer H. A virtual structure approach to formation control of unicyle mobile robots using mutual coupling. International Journal of Control 84(11)2011;:1886–1902. http://dx.doi.org/10.1080/00207179.2011.627686.Xiang, X. Lapierre, L., Bruno, J., Parodi, O., 2010. Coordinated Formation Control of Multiple Autonomous Underwater Vehicles for Pipeline Inspection. International Journal of Advanced Robotic Systems. 7(1), 75-84.
Xiang X., Lapierre L., Bruno J., Parodi O. Coordinated Formation Control of Multiple Autonomous Underwater Vehicles for Pipeline Inspection. International Journal of Advanced Robotic Systems 7(1)2010;:75–84.