|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(2); 2018 > Article |
|
Abstract
Dean's equilibrium beach profile formula was used to investigate the correlation between the static shoreline position and the incident wave energy. The effect of the longshore sediment transport was neglected, and the results showed the reasonable agreement compared with the field observations of Yates et al.(2009), which were conducted for almost 5 years on southern California beaches, USA. The shoreline response varies with the scale factor of Dean's equilibrium beach profile. This implies that the shoreline response could be simply estimated using the sampled grain size without laborious long-term field work. Therefore, the present study results are expected to be practically used for the layout design of submerged or exposed detached breakwaters although the further work is required for performance verification. In addition, after laborous mathematical reviews, the linear relation between incident energy and shoreline response, which was obtained from YatesвАЩs field study, yielded a clear mathematical equation showing how the beach slope is related to the grain size.
мµЬкЈЉ мЧ∞мХИмЧРмДЬ лєИл≤ИнЮИ л∞ЬмГЭнХШлКФ мє®мЛЭлђЄм†Ьк∞А мВђнЪМм†Б мЭімКИл°Ь нБђк≤М лМАлСРлРШк≥†, мЭіл•Љ мШИл∞© лШРлКФ л∞©мІАнХШк≥†мЮР нХШлКФ л™®лЛИнД∞лІБ л∞П мє®мЛЭм†Ак∞Р кЄ∞мИ†мЭШ нХДмЪФмД±мЭі м¶ЭлМАлРШк≥† мЮИлЛ§. кЈЄлЯђлВШ мЭілЯђнХЬ л™®лЛИнД∞лІБ мЮРл£МмЭШ лґДмДЭмЭілВШ мє®мЛЭм†Ак∞Р кЄ∞мИ†мЭШ мВђм†Д нГАлЛємД±мЭД нПЙк∞АнХ†лІМнХЬ мЛ§мІИм†БмЭЄ мЧ∞кµђ мД±к≥ЉлКФ кµ≠лВілњРлІМ мХДлЛИлЭЉ м†Д мДЄк≥Дм†БмЬЉл°ЬлПД мХДмІБ лІМм°±нХ† лІМнХЬ мИШм§АмЧР лПДлЛђнХШмІА л™їнХШк≥† мЮИлЛ§. л≥Є мЧ∞кµђмЧРмДЬлКФ нММлЮС мЧРлДИмІАл•Љ м†ЬмЦінХШмЧђ нЪ°лЛ®нСЬмВђл°Ь мЭЄнХШмЧђ л∞ЬмГЭнХШлКФ мє®мЛЭ лђЄм†Ьл•Љ нХік≤∞нХШкЄ∞ мЬДнХЬ мИШлЛ®мЬЉл°Ь к≤АнЖ†лРШлКФ мЭімХИм†ЬлВШ мЮ†м†Ь лУ±мЭШ нХімХИкµђм°∞лђЉмЭі нХімХИмД† мє®мЛЭмЭД мЦЉлІИлВШ нЪ®к≥Љм†БмЬЉл°Ь м†ЬмЦінХ† мИШ мЮИлКФмІАл•Љ м†ХлЯЙм†БмЬЉл°Ь нПЙк∞АнХШлКФ лН∞ мЬ†мЪ©нХЬ л∞©л≤Хл°†мЭД м†ЬмЛЬнХЬлЛ§.
мЧ∞мХИмЧ≠мЧРмДЬ л™®лЮШ, мЮРк∞И лУ± нЗім†БлђЉмЭі мМУмЧђ мЮИлКФ к≥≥мЭД нХілєИмЭілЭЉк≥† нХШл©∞, нХілєИмЭА нММлЮС, нП≠нТН лУ± к≥Дм†Им†БмЭЄ мЪФмЭЄмЧР лФ∞л•Є нММлЮСк≥Љ л∞ФлЮМмЭШ л≥АнЩФмЩА мИШмЛ≠вЛЕмИШл∞± лЕДмЭШ кЄ∞нЫД л∞П нХімИШл©і л≥АнЩФ лУ± лЛ§мЦСнХЬ л≤ФмЬДмЧРмДЬ нЗім†БлђЉ к≥µкЄЙк≥Љ мЪіл∞Ш мВђмЭімЭШ мГБнШЄ мЮСмЪ©мЧР мЭШнХі л∞ЬлЛђнХЬлЛ§. кЈЄ м§СмЧРмДЬлПД мЮРмЧ∞м†БмЭЄ нХілєИмЭШ нШХмД±к≥Љ л≥АнЩФмЧР мЮИмЦі нММлЮСмЭШ мШБнЦ•мЭА лІ§мЪ∞ м§СмЪФнХЬ мЪФмЭЄмЭілЛ§.
нММлЮС мЧРлДИмІАмЩА нХімХИмД† л≥АнЩФлКФ л∞Ам†СнХЬ кіА놮мЭі мЮИлЛ§. нММлЮС мЧРлДИмІАмЧР лФ∞лЭЉ нШХмД±лРШлКФ нЪ°лЛ®нСЬмВђмЭШ мЬ†мЮЕк≥Љ мЬ†мґЬмЭШ л≥АнЩФмЧР мЭШнХШмЧђ нХімХИмД†мЭШ л≥АнЩФк∞А міИлЮШлРЬлЛ§. нЪ°лЛ®нСЬмВђлКФ нХімХИмД†к≥Љ мИШмІБл∞©нЦ•мЬЉл°Ь мЭілПЩнХШлКФ нСЬмВђл•Љ лІРнХШл©∞, мЧ∞мХИмЧ≠мЬЉл°Ь нЪ°лЛ®нСЬмВђ мЬ†мЮЕк≥Љ мЬ†мґЬмЭШ кіАк≥ДмЧР лФ∞лЭЉ нХілєИмЭШ мє®мЛЭк≥Љ нЗім†Б нКємД±мЭі к≤∞м†ХлРШл©∞, к≤∞к≥Љм†БмЬЉл°Ь нХімХИмД†мЭі м†ДмІДнХШк≥† нЫДнЗінХШлКФ лУ±мЭШ л∞ШмЭСмЭД мЭЉмЬЉнВ®лЛ§. мЭЉл∞Шм†БмЬЉл°Ь нММлЮС мЧРлДИмІАк∞А лВЃмЭА мЧђл¶Дм≤†мЧРлКФ мЧ∞мХИмЬЉл°ЬмЭШ нЪ°лЛ®нСЬмВђк∞А мЪ∞мЫФнХШмЧђ нХімХИмД†мЭі м†ДмІДнХШк≥† нММлЮС мЧРлДИмІАк∞А нБ∞ к≤®мЪЄм≤†мЧРлКФ нХілєИлЛ®мЭШ м†Дл©імЭі кєОмЭіл©∞, мЩЄнХіл°ЬмЭШ нЪ°лЛ®нСЬмВђк∞А л∞ЬмГЭнХШмЧђ нХімХИмД†мЭі нЫДнЗінХШлКФ мє®мЛЭмЭі л∞ЬмГЭнХЬлЛ§(Kim and Lee, 2015).
нММлЮС мЧРлДИмІА мЬ†мЮЕмЧР мЭШнХЬ нХімХИмД†мЭШ м†ДмІД лШРлКФ нЫДнЗі лУ±мЭШ л∞ШмЭСмЭА Larson and Kraus(1989)мЧР мЭШнХШмЧђ мЭіл°†м†БмЬЉл°Ь м≤ШмЭМ м†ЬмХИлРШмЧИлЛ§. кЈЄ нЫД Dean(1991)мЭА мЦСлєИ нФДл°Ьм†ЭнКЄмЧР м†БмЪ©нХШмЧђ мЭіл°†м†Б нГАлЛємД±мЭД к≤Ам¶ЭнХШмШАк≥†, Kriebel and Dean(1993)к≥Љ Miller and Dean(2004)мЭА нП≠нТНмЧР мЭШнХЬ нШДмІА нХімХИмД† л∞ШмЭСмЧР лМАнХЬ л™®лНЄлІБмЬЉл°Ь нЩХмЮ•нХШмШАлЛ§. мµЬкЈЉмЧР Yates et al.(2009)мЭА нХілєИмЭі мІАмЖНм†БмЬЉл°Ь нММлЮС мЧРлДИмІАмЧР лЕЄмґЬлРШлКФ к≤љмЪ∞ к≥†мЬ†нХЬ нХімХИмД† мЬДмєШл°Ь мИШл†інХ† к≤ГмЭілЭЉлКФ к∞Ам†Х нХШмЧР мХљ 65kmмЧР лЛђнХШлКФ лѓЄкµ≠ мДЬлґА мЇШл¶ђнПђлЛИмХД нХіл≥АмЧРмДЬ мХљ 5лЕДк∞Д нММлЮС мЧРлДИмІА, нПЙкЈ†нХімИШл©і, нХілєИмЄ°лЯЙ кЈЄл¶ђк≥† кЈЄмЧР лФ∞л•Є нХімХИмД†мЭШ м†ДмІД лШРлКФ нЫДнЗі мЦСмГБмЧР лМАнХЬ нШДмЮ•кіАмЄ°мЭД мИШнЦЙнХШмШАлЛ§.
л≥Є мЧ∞кµђмЧРмДЬлКФ мЬ†мЮЕ нММлЮС мЧРлДИмІАмЩА нХімХИмД† мЬДмєШмЭШ л≥АнЩФмЧР лМАнХЬ мГБкіАкіАк≥Дл•Љ лґДмДЭ нХШлКФ к≥Љм†ХмЧРмДЬ нПЙнШХ нХілєИ лЛ®л©і мЭіл°†мЭД м†БмЪ©нХЬлЛ§. мЭі мЭіл°†мЭА м≤ШмЭМ нХімХИ мҐЕл∞©нЦ•(Cross-shore)мЬЉл°ЬмЭШ нСЬмВђмЭілПЩк≥Љ кіА놮нХШмЧђ Bruun(1954)мЩА Bruun(1962)мЧР мЭШнХШмЧђ м†ЬмЛЬлРШмЧИлЛ§. кЈЄ нЫД нПЙнШХнХілєИлЛ®л©і мЭіл°†мЭА міИкЄ∞ мІБмД†м†Б нХілєИ лЛ®л©імЧР лМАнХЬ мє®мЛЭ нП≠ мґФм†Х(Suh and Dalrymple, 1988), нХілєИлЛ®л©імЭШ мЭСлЛµл™®нШХ(Larson and Kraus, 1989)к≥Љ мЦСлєИ нФДл°Ьм†ЭнКЄмЧРмЭШ м†БмЪ©(Dean, 1991), мВђкµђмЧРмДЬмЭШ нХілєИлЛ®л©імЭШ мЛЬк∞Дм†Б л≥АнЩФ(Plant et al., 1999), нХімИШл©і мГБмКємЧР мЭШнХЬ нХілєИлЛ®л©імЭШ л≥АнЩФ(Dubois, 1990), нП≠нТНнХімЭЉ(Kriebel and Dean, 1993)к≥Љ нП≠нТН(Miller and Dean, 2004) лУ±мЧР мЭШнХЬ нХілєИлЛ®л©імЭШ мЛЬк∞Дм†Б л≥АнЩФ лУ±мЭД мШИмЄ°нХШлКФ мЛ§мІИм†БмЭЄ к∞ЬлЕРмЬЉл°Ь лДРл¶ђ м†БмЪ©лРШмЦі мЩФлЛ§.
нХімХИмД† л≥АнЩФ л∞П нПЙнШХнХілєИлЛ®л©імЧР кіАнХЬ мЪ∞л¶ђлВШлЭЉ мЧ∞кµђ мВђл°Ал•Љ мВінОіл≥іл©і нХімХИмД† л≥АнШХ мШИмЄ°мЧР лМАнХЬ мИШмєШл™®лНЄ мЧ∞кµђ(Park et al., 1993), нХімИШл©і мГБмКємЧР мЭШнХЬ нХімХИмД†мЭШ мЮ†мЮђм†Б нЫДнЗік±∞л¶ђмЭШ мВ∞м†Х(Son, 1993), нЪ°лЛ®нСЬмВђмЧР лФ∞л•Є нХімХИмД† л≥АнЩФмЧР кіАнХЬ мЛ§нЧШм†Б мЧ∞кµђ(Son and Lee, 2000), к∞ХмЫРлПД нХімИШмЪХмЮ•мЭШ мЬ†мШБнП≠ л∞П нХілєИлЛ®л©і мґХм≤Щк≥ДмИШ м°∞мВђ лґДмДЭ(Lee and Kim, 2006) кЈЄл¶ђк≥† нХілєИ мҐЕлЛ®л©і л≥АнШХмЭШ мИШмєШл™®мЭШ(Cheon and Ahn, 2008) лУ±мЧР лМАнХЬ мЧ∞кµђк∞А мИШнЦЙлРШмЧИлЛ§. кЈЄлЯђлВШ мД†мІДкµ≠мЧР лєДнХШл©і мХДмІБ лѓЄлєДнХШл©∞ мЛ§м†Ь мЧ∞мХИмє®мЛЭмЭД мЩДнЩФмЛЬнВ§кЄ∞ мЬДнХЬ нХімХИкµђм°∞лђЉмЭШ кµђм°∞мД§к≥Д л∞П л∞∞мєШмД§к≥Д лУ±мЭШ м†БмЪ© мВђл°АмЧР лМАнХЬ мЧ∞кµђк∞А нШДмЮђкєМмІАлКФ лґАм°±нХШлЛ§. кЈЄл°Ь мЭЄнХШмЧђ мЦСлєИ лШРлКФ мЪ∞нЪМмЦСлєИ(Sand bypassing) лУ± мЭЄмЬДм†Б нХілєИм°∞мД± к≥µл≤ХмЭілВШ лПМм†Ь лШРлКФ мЮ†м†Ь лУ±мЭШ лІОмЭА нХімХИкµђм°∞лђЉмЭі мД§мєШлРШк≥† мЮИмЭМмЧРлПД нШДмЮђкєМмІА мД±к≥µм†БмЭЄ к≤ГмЬЉл°Ь нПЙк∞АлРШлКФ мВђмЧЕмВђл°Ак∞А лєДкµРм†Б лУЬлђЄ лІМнБЉ мЭімЧР лМАнХЬ мІАмЖНм†БмЭЄ мЧ∞кµђк∞А нХДмЪФнХЬ мЛ§м†ХмЭілЛ§.
л≥Є мЧ∞кµђмЧРмДЬлКФ Dean(1977)мЭШ нПЙнШХнХілєИлЛ®л©імЭШ к∞ЬлЕРмЭД мЭімЪ©нХШмЧђ мЬ†мЮЕлРШлКФ нММлЮС мЧРлДИмІАмЧР лФ∞лЭЉ мИШл†інХШлКФ к≥†мЬ†нХЬ нХімХИмД† мЬДмєШ к∞ДмЭШ л≥АнЩФкіАк≥Дл•Љ лґДмДЭнХЬлЛ§. мЧ∞мХИнСЬмВђмЧР лФ∞л•Є мШБнЦ•мЭА лђімЛЬнХШмШАмЬЉл©∞, Yates et al.(2009)мЭШ нШДмЮ•кіАмЄ° к≤∞к≥ЉмЩА лєДкµРнХШк≥†, кЈЄ к∞ЬлЕРмЭШ нГАлЛємД±мЭД лШРнХЬ к≤Ам¶ЭнХЬлЛ§. Yates et al.(2009)мЭА 5лЕДк∞ДмЭШ нШДмЮ• кіАмЄ°мЬЉл°ЬлґАнД∞ мЬ†мЮЕлРШлКФ нММлЮС мЧРлДИмІАмЧР лФ∞л•Є к≥†мЬ†нХЬ нХімХИмД† мЬДмєШмЧР лМАнХЬ кіАк≥ДмЛЭмЭД мЦїмЦілГИмІАлІМ л™®лУ† нХімХИмЧР лМАнХШмЧђ мЭілЯђнХЬ кіАмЄ°мЭі мИШнЦЙлРШмІА мХКк≥†лКФ кЈЄ кіАк≥Дл•Љ л™ЕнЩХнЮИ нММмХЕнХШкЄ∞ мֳ놵кЄ∞ лХМлђЄмЧР л≥Є мЧ∞кµђмЧРмДЬлКФ кіАмЄ°мЭД мИШнЦЙнХШмІА мХКк≥†лПД нХілєИ мЮЕмЮР нКємД±мЬЉл°ЬлґАнД∞ кЈЄ кіАк≥Дл•Љ мЦїмЦілВілКФ л∞©л≤Хл°†мЭД м†ЬмЛЬнХЬлЛ§.
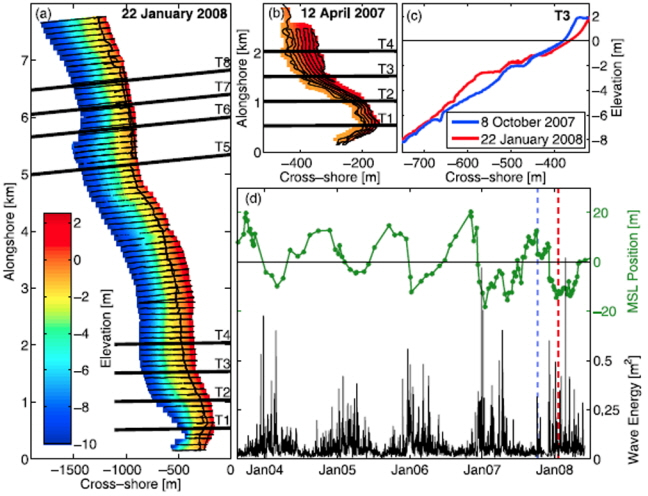
Yates et al.(2009)мЭА мЬ†мЮЕлРШлКФ нММлЮС мЧРлДИмІАмЧР лФ∞лЭЉ нХімХИмД†мЭШ мЬДмєШк∞А мЦілЦїк≤М л∞ШмЭСнХШлКФ мІАмЧР лМАнХЬ мЧ∞кµђл•Љ мИШнЦЙнХШкЄ∞ мЬДнХШмЧђ Fig. 1к≥Љ к∞ЩмЭі лѓЄкµ≠ мЉИл¶ђнПђлЛИмХДм£ЉмЭШ San Diego CountyмЧР мЬДмєШнХЬ кЄЄмЭі мХљ 65гОЮмЧР лЛђнХШлКФ нХімХИмЭШ 4к∞Ь мІАм†Р(Torrey Pines, Cardiff, Camp Pendleton and San Onofre)мЧРмДЬмЭШ нММлЮС кіАмЄ°к≥Љ нХілєИ мЄ°лЯЙ лУ± м£ЉкЄ∞м†БмЭЄ л™®лЛИнД∞лІБмЭД мЛ§мЛЬнХШмШАлЛ§. м°∞мВђмЮ•мЖМмЧР лМАнХЬ мЭЉл∞Шм†БмЭЄ нКємД±(нХілєИ нП≠, нХілєИк≤љмВђ, л™®лЮШмЮЕк≤љ лУ±)мЭА Table 1мЧР м†ЬмЛЬлРШмЧИлЛ§. л™®лУ† нХіл≥АмЧРмДЬмЭШ мЖМм°∞мЩА лМАм°∞лКФ лМАлЮµ 1.0m л∞П 2.5mмЭЄ к≤ГмЬЉл°Ь нММмХЕлРШмЧИлЛ§.
Fig. 2лКФ 4к∞Ь мІАм†Р к∞АмЪілН∞ Torrey PinesмЧРмДЬмЭШ нХілєИ мЄ°лЯЙ к≤∞к≥ЉмЩА мИШмЛђ 10mмЧРмДЬ кіАмЄ°лРЬ нММлЮС мЮРл£М, кЈЄл¶ђк≥† нХімХИмД†мЭШ л≥АлПЩмЧР лМАнХЬ мГБмДЄнХЬ к≤∞к≥Љл•Љ л≥імЧђм§АлЛ§. нХілєИ мЄ°лЯЙ мЮРл£МлКФ м£Љ лШРлКФ мЫФл≥Д кіАмЄ° мЮРл£МмЭШ мЫФнПЙкЈ† к∞ТмЬЉл°Ь м†ЬмЛЬлРШмЧИмЬЉл©∞ нММлЮС кіАмЄ° мЮРл£МлКФ мК§нОЩнКЄлЯЉ мЮРл£МмЭШ мЛЬк∞ДлЛє нПЙкЈ†к∞ТмЬЉл°Ь м†ЬмЛЬлРШмЧИлЛ§. 2007лЕД 4мЫФк≥Љ 2008лЕД 1мЫФмЧР мЛ§мЛЬлРЬ нХілєИ мЄ°лЯЙ к≤∞к≥Љк∞А к∞Бк∞Б м†ЬмЛЬлРШмЧИмЬЉл©∞ лШРнХЬ 2007лЕД 10мЫФ 22мЭЉмЧР кіАмЄ°лРЬ нХілєИ мҐЕлЛ®л©і кЄ∞м§Ам†Р T3мЧРмДЬмЭШ нХілєИлЛ®л©і мЄ°лЯЙ к≤∞к≥Љк∞А 3к∞ЬмЫФ нЫДмЭЄ 2008лЕД 1мЫФ 22мЭЉмЧР лПЩмЭЉ кЄ∞м§Ам†РмЧРмДЬ кіАмЄ°лРЬ нХілєИлЛ®л©і мЮРл£МмЩА мДЬл°Ь лєДкµРлРШмЧИлЛ§. Torrey PinesмЭШ нХімХИмЧРмДЬ 500m к∞Дк≤©мЬЉл°Ь 4kmмЧР к±Єм≥Р T1лґАнД∞ T8кєМмІАмЭШ кЄ∞м§Ам†РмЧР лМАнХШмЧђ кіАмЄ°мЭі мИШнЦЙлРШмЧИлЛ§. Fig. 2мЭШ мЪ∞мЄ° нХШлЛ®мЧР м†ЬмЛЬлРЬ нММлЮС мЧРлДИмІА кіАмЄ° мЮРл£Мл•Љ мВінОіл≥іл©і к≥Дм†Им†Б л≥АлПЩмД±мЭД л≥імЭік≥† мЮИмЬЉл©∞ мЭіл°Ь мЭЄнХШмЧђ мЪ∞мЄ° мГБлЛ®мЧР мДЬл°Ь лєДкµРлРЬ нХілєИлЛ®л©і к≤∞к≥ЉмЧРмДЬмЩА к∞ЩмЭі нХімХИмД†мЭі нЫДнЗілРШк≥† лМАмЛ† мЗДнММм†Р м£Љл≥АмЧРмДЬ мЧ∞мХИ мВђм£Љк∞А нШХмД±лРЬ л™®мКµмЭД л≥імЧђм£Љк≥† мЮИлЛ§.
мЬ†мЮЕ нММлЮС мЧРлДИмІА E мЧР лФ∞лЭЉмДЬ нХімХИмД† мЬДмєШ MSL(Mean sea level)мЧРмДЬмЭШ нХімХИмД† м†ДмІДмЭілВШ нЫДнЗі к≤љнЦ•мЭД мВінХА нЫД нЫДнЗі(Erosion)л•Љ лє®к∞ДмГЙ, м†ДмІД(Accretion)мЭД нММлЮАмГЙмЬЉл°Ь нСЬкЄ∞нХШл©і нЫДнЗімЩА м†ДмІДмЭі л∞ЬмГЭнХШмІА мХКлКФ к≤љк≥Дл•Љ нММмХЕнХ† мИШ мЮИлЛ§. Fig. 3мЧРмДЬ л≥імЭілКФ к≤Гк≥Љ к∞ЩмЭі нЫДнЗімЩА м†ДмІДмЭі л∞ЬмГЭнХШмІА мХКлКФ к≤љк≥Дл•Љ к≤Ам†ХмГЙ мД†мЬЉл°Ь кЈЄл¶і мИШ мЮИк≥†, мЭі мД†мЭА мЬ†мЮЕлРШлКФ нММлЮС мЧРлДИмІАмЧР лМАнХШмЧђ мИШл†ілРШлКФ нХімХИмД† мЬДмєШмЭЄ к≤ГмЬЉл°Ь мґФм†ХнХ† мИШ мЮИлЛ§.
лФ∞лЭЉмДЬ мЭілЯђнХЬ кіАк≥ДмЛЭмЭД мЦїмЬЉл©і мЬ†мЮЕ нММлЮС мЧРлДИмІАмЧР лФ∞лЭЉмДЬ нХімХИмД†мЭі мЦілЦїк≤М л∞ШмЭСнХ† мІАл•Љ лѓЄл¶ђ мШИмЄ°нХ† мИШ мЮИмЬЉлѓАл°Ь мІАлВШмєШк≤М нХімХИмД†мЭі нЫДнЗінХШлКФ нХімХИмЧРмДЬ к≥†нММлЮСмЭД м†ЬмЦінХШлКФ мЮ†м†ЬлВШ мЭімХИм†Ь лУ±мЭШ нХімХИкµђм°∞лђЉмЭД лСРмЦі л∞∞нЫД нХімХИмЬЉл°ЬмЭШ нММлЮС мЧРлДИмІА мЬ†мЮЕмЭД к∞РмЖМмЛЬмЉЬ нХімХИмД† нЫДнЗіл•Љ м†ЬмЦінХ† мИШ мЮИк≤М лРЬлЛ§. мЭілЯђнХЬ м†СкЈЉ л∞©л≤ХмЧРмДЬ мЧ∞мХИ нСЬмВђл°Ь мЭЄнХЬ мШБнЦ•мЭА лђімЛЬлРШл©∞ мЧ∞мХИнСЬмВђмЭШ мШБнЦ•мЭі нПђнХ®лРЬлЛ§л©і нХімХИмД†мЭШ л≥АлПЩ нП≠мЭА лМАлґАлґД лНФ лКШмЦілВШлКФ к≤ГмЬЉл°Ь к∞Дм£ЉлР† мИШ мЮИлЛ§.
лФ∞лЭЉмДЬ Fig. 3мЬЉл°ЬлґАнД∞ нММлЮС мЧРлДИмІА Eк∞А мІАмЖНм†БмЬЉл°Ь мЬ†мЮЕлРШлКФ к≤љмЪ∞ нХімХИмД†мЭі кґБкЈєм†БмЬЉл°Ь нПЙнШХнХімХИмД†мЭШ мЬДмєШ Seq л°Ь мИШл†ілРШлКФлН∞ мЭіл•Љ мІБмД†мЭілЭЉк≥† к∞Ам†ХнХШл©і лЛ§мЭМк≥Љ к∞ЩлЛ§.
мЧђкЄ∞мДЬ мЬ†мЮЕнММлЮС мЧРлДИмІА EлКФ лґИкЈЬмєЩ нММмЭШ к≤љмЪ∞ мХДлЮШмЩА к∞ЩмЭі мЬ†мЭШнММк≥† HsмЭШ нХ®мИШл°Ь м†ХмЭШлРЬлЛ§.
кЈЄл¶ђк≥† aмЩА bлКФ Sл•Љ к∞Ал°ЬмґХмЬЉл°Ь лСШ лХМ к∞Бк∞Б мІБмД†мЭШ к≤љмВђмЩА м†ИнОЄмЭі лРЬлЛ§. S=0мЭЄ нХімХИмД† мЬДмєШлКФ мЧ∞нПЙкЈ† нММлЮС мЧРлДИмІА E b ¬ѓ b = E b ¬ѓ
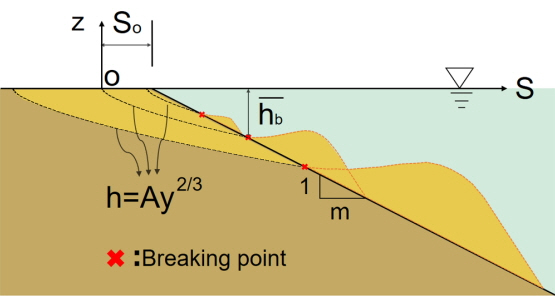
Dean(1977)мЭА Florida Peninsula кЈЉл∞©мЭШ Long IslandмЭШ лПЩм™љ лБЭмЧРмДЬлґАнД∞ Texas-Mexico м†Ск≤љмІАмЧ≠кєМмІА лѓЄкµ≠ 502к∞ЬмЭШ нХілєИлЛ®л©імЧР лМАнХЬ нШДмІАмЄ°лЯЙмЭД мЛ§мЛЬнХШмШАмЬЉл©∞ к∞Б нХілєИлЛ®л©і мЮРл£Мл•Љ мЈ®нХ©нХШк≥† к∞АмЮ• мЮШ FittingнХШлКФ л≥інОЄм†Б нХілєИлЛ®л©і нШХмГБмЭД мЛЭ (3)мЩА к∞ЩмЭі мЬ†мЭЉнХЬ к≥ДмИШмЭЄ нХілєИмґХм≤Щк≥ДмИШ Aл°Ь нСЬнШДлРШлКФ мЛЭмЭД м†ЬмХИнХШмШАлЛ§.
мЧђкЄ∞мДЬ h(y)лКФ мИШмЛђ, y лКФ нХімХИмД†мЧРмДЬлґАнД∞мЭШ мЭімХИк±∞л¶ђ, AлКФ нХілєИмґХм≤Щк≥ДмИШ(Beach scale factor)л°Ь мЮЕк≤љмЧР мЭШм°інХШлКФ к≥ДмИШмЭіл©∞ лЛ®мЬДлКФ m1/3мЭілЛ§. нХілєИмґХм≤Щк≥ДмИШ AлКФ м§СмХЩмЮЕк≤љк≥Љ л∞Ам†СнХЬ кіАк≥Дк∞А мЮИлКФ к≥ДмИШл°ЬмДЬ мЭіл•Љ мґФм†ХнХШлКФ л∞©л≤ХмЭА лЛ§мЦСнХШлЛ§. Moore(1982)лКФ нЖ†мВђмЭШ мЬ†нЪ® нБђкЄ∞ мВђмЭімЭШ мГБкіАкіАк≥Дл•Љ м†ХлЯЙнЩФнХШкЄ∞ мЬДнХі мИШлІОмЭА лЛ®л©ім°∞мВђл•Љ нЦИк≥†, лґДмДЭмЧР лФ∞л•іл©і к∞АнММл•Є лЛ®л©ік≥Љ м°∞к∞ЬкїНмІИмЭі лМАлґАлґДмЭЄ к∞Ал≤ЉмЪі л™®лЮШмІИмЭШ нХілєИлЛ®л©імЧР лМАнХімДЬлПД мЮШ м†БмЪ©лРШмЧИлЛ§. Dean et al.(2001)мЭА нЗім†БлђЉмЭШ м§СмХЩмЮЕк≤љ D50мЭШ нБђкЄ∞л•Љ 0.01mmмЭШ к∞Дк≤©мЬЉл°Ь 0.1mmл°ЬлґАнД∞ 1.09mmкєМмІАмЭШ A к∞ТмЭД Table 2мЧР м†ЬмЛЬнХШмШАлЛ§.
нПЙнШХнХілєИлЛ®л©імЛЭмЭА мЗДнММлМА лВімЧРмДЬ м†БмЪ©лРШлКФ мЛЭмЭілѓАл°Ь кЈЄ мЛЭмЭШ м†БмЪ© нХЬк≥ДлКФ нХімХИмД†мЬЉл°ЬлґАнД∞ мЗДнММм†Р(Breaking point)кєМмІАмЭілЛ§. кЈЄлЯђлѓАл°Ь нММк≥†мЧР лФ∞лЭЉмДЬ лЛђлЭЉмІАлКФ мЗДнММм†РмЭі мЮДмЭШмЭШ нХілєИ к≤љмВђл•Љ лФ∞лЭЉ л∞ЬмГЭнХЬлЛ§к≥† к∞Ам†ХнХШл©і мИШл†інХімХИмД†мЭШ мЬДмєШл•Љ кµђнХ† мИШ мЮИлЛ§. мЗДнММк≥† HbмЧР лМАнХШмЧђ мЗДнММк∞А мЛЬмЮСлРШлКФ мИШмЛђ HbмЭД мВ∞м†ХнХШкЄ∞ мЬДнХШмЧђ к∞АмЮ• к∞ДлЛ®нХШл©імДЬлПД лДРл¶ђ мВђмЪ©лРШлКФ Miche(1944)мЭШ мИШмЛЭмЭД м†БмЪ©нХШмШАлЛ§.
мЧђкЄ∞мДЬ мХДлЮШм≤®мЮР bлКФ мЗДнММм†РмЧРмДЬмЭШ к∞ТмЭД мЭШлѓЄнХШл©∞ ќ≥лКФ 0.7~1.3мЭШ л≤ФмЬДл•Љ к∞ЦлКФ к∞ТмЬЉл°Ь мЧђкЄ∞мДЬлКФ нПЙмГБнММмЧР м†БмЪ©лРШлКФ ќ≥=0.78мЭД мВђмЪ©нХШмШАлЛ§. мЛЭ (4)л•Љ м†БмЪ©нХШк≥† Dean(1977)мЭШ нПЙнШХнХілєИлЛ®л©імЛЭмЭД мЭімЪ©нХШл©і Fig. 4мЭШ yкЄ∞м§Ам†РмЬЉл°ЬлґАнД∞ нХімХИмД†мЭШ л≥АнЩФ нП≠мЭЄ вИЖyл•Љ мХДлЮШмЩА к∞ЩмЭі мВ∞мґЬнХ† мИШ мЮИлЛ§.
мЧђкЄ∞мДЬ mмЭА Fig. 4мЧР лПДмЛЬлРЬ л∞ФмЩА к∞ЩмЭі нПЙнШХнХілєИлЛ®л©імЛЭмЭі мЬ†нЪ®нХЬ мЩЄнХі нХЬк≥Дм†Р м¶Й, мЗДнММ мЛЬмЮСм†РмЭД мЧ∞к≤∞нХЬ мД†мЭШ к≤љмВђл°ЬмДЬ мІБмД†мЭЄ к≤ГмЬЉл°Ь к∞Ам†ХлРШмЧИлЛ§.
Fig. 4мЧРмДЬ мИШл†інХімХИмД† мЬДмєШмЭШ л≥АнЩФл•Љ лВШнГАлВілКФ Sк∞А нММлЮС мЧРлДИмІАк∞А 0мЭЄ к≤љмЪ∞мЧР мИШл†ілРШлКФ нХімХИмД† мЬДмєШк∞А кЄ∞м§АмЭі лРШлКФ к≤ГмЭі мХДлЛИлЭЉ к∞АмЮ• лєИлПДк∞А лЖТмЭА нММлЮС мЧРлДИмІАмЭЄ нПЙкЈ† нММлЮС мЧРлДИмІАмЧР мЭШнХШмЧђ мИШл†ілРШлКФ нХімХИмД†мЭШ мЬДмєШмЭЄ Oм†РмЭі кЄ∞м§АмЭі лРЬлЛ§л©і мИШл†інХімХИмД† мЬДмєШ SeqмЧР лМАнХЬ мЛЭмЭА мХДлЮШ мЛЭк≥Љ к∞ЩмЭі м£ЉмЦімІДлЛ§.
Fig. 4мЧРмДЬ SoлКФ нММлЮС мЧРлДИмІАк∞А к±∞мЭШ мЬ†мЮЕлРШмІА мХКлКФ мГБнГЬмЭШ нПЙнШХнХімХИмД† мЬДмєШл°ЬмДЬ м≤ЬмИШ нЪ®к≥Љл•Љ лђімЛЬнХШл©і мЛЭ (1)мЧРмДЬ -b/aмЧР нХілЛєлРШлКФ к∞ТмЭіл©∞ мЛЭ (6)мЧРмДЬ hb=0мЬЉл°Ь лСРл©і мЦїмЭД мИШ мЮИлКФ к∞ТмЭілЛ§. м¶Й,
мЛЭ (8)мЭШ лМАкіДнШЄ мХИмЭШ к∞ТмЭА -1/aмЧР нХілЛєлРШл©∞ кіАмЄ° к≤∞к≥ЉмЧР лФ∞л•іл©і мЭі к≤∞к≥ЉлКФ мЬ†мЮЕ мЧРлДИмІАмЧР кіАк≥ДмЧЖмЭі к±∞мЭШ мЭЉм†ХнХЬ к∞ТмЬЉл°Ь мґФм†ХлРШмЧИлЛ§. лФ∞лЭЉмДЬ лЛ§мЭМк≥Љ к∞ЩмЭі мЛЭ (1)к≥Љ мЬ†мВђнХЬ мЛЭмЬЉл°Ь л≥АнЩШлР† мИШ мЮИлЛ§.
Fig. 3к≥Љ к∞ЩмЭі мЛЭ (8)мЧРмДЬ лМАкіДнШЄ мХИмЭШ к∞ТмЭі мЬ†мЮЕ мЧРлДИмІАмЧР кіАк≥ДмЧЖмЭі к±∞мЭШ мЭЉм†ХнХЬ к∞ТмЭі лРЬлЛ§л©і нХілєИк≤љмВђ mмЭі Scale factor AмЩА мЦілЦ§ кіАк≥Дк∞А мЮИлКФмІАл•Љ лШРнХЬ нМРлЛ®нХ† мИШ мЮИлЛ§. лЛ§мЖМ кєМлЛ§л°ЬмЪі мИШнХЩм†Б к≤АнЖ† нЫД нХілєИ к≤љмВђмЩА мґХм≤Щ к≥ДмИШк∞ДмЭШ кіАк≥Дк∞А мХДлЮШмЩА к∞ЩмЭА к≤љмЪ∞ мИШмЛђмЭШ мШБнЦ•мЭД лНЬ л∞Ык≥† к±∞мЭШ мЭЉм†ХнХЬ к∞ТмЭД м†Ьк≥µнХШлКФ к≤ГмЬЉл°Ь нМРлЛ®лРШмЧИлЛ§.
мЧђкЄ∞мДЬ fлКФ нХіл≥А м°∞к±ік≥Љ кіАк≥ДмЧЖмЭі к±∞мЭШ мЭЉм†ХнХЬ мГБмИШмЭЄ к≤ГмЬЉл°Ь к∞Дм£ЉлР† мИШ мЮИлЛ§. мЛЭ (11)мЭА лШРнХЬ нХілєИк≤љмВђ mмЭШ нХ®мИШл°ЬлПД мХДлЮШмЩА к∞ЩмЭі м£ЉмЦімІДлЛ§.
лФ∞лЭЉмДЬ Table 1мЧР м†ЬмЛЬлРЬ нХілєИ к≤љмВђмЩА мЮЕк≤љ мЮРл£Мл•Љ мЭімЪ©нХШмЧђ мЛЭ (9)л°ЬлґАнД∞ fл•Љ мґФмВ∞нХШк≥† нПЙкЈ†мЭД кµђнХШл©і мХљ 1.17мЭШ нПЙкЈ†к∞ТмЭД к∞ЦлКФлЛ§. к≥ДмВ∞ к≥Љм†ХмЭА Table 2мЧР м†ЬмЛЬлРШмЧИлЛ§. fмЭШ к∞ТмЭі 0.86лґАнД∞ 1.80кєМмІА нБ∞ л≥АнЩФл•Љ л≥імЭік≥† мЮИлЛ§. Table 1мЧРмДЬмЩА к∞ЩмЭі нХілєИ к≤љмВђк∞А лМАлЮµм†БмЬЉл°Ь м†ЬмЛЬлРШмЧИмЬЉл©∞ нХілєИ к≤љмВђмЩА м§СмХЩ мЮЕк≤љ мЮРл£Мл•Љ мДЬл°Ь лєДкµРнХШмШАмЭД лХМ нХілєИ к≤љмВђк∞А кЄЙнХ†мИШл°Э мЮЕк≤љмЭі мї§мІАлКФ л≥інОЄм†БмЭЄ к≤љнЦ•мЭі лІМм°±лРШмІА л™їнХШк≥† мЮИлЛ§. лФ∞лЭЉмДЬ мЬ†мЮЕ нММк≥†мЧР лФ∞лЭЉ лґАмЬ†мВђ мЭілПЩмЭі мЛђнХЬ м†РмЭД к≥†л†§нХШл©і MSLмЧРмДЬмЭШ л™®лЮШ мЮЕк≤љмЭШ лМАнСЬмД±мЭі нХілєИ к≤љмВђмЧР лєДнХШмЧђ лґАм°±нХ† мИШлПД мЮИлЛ§к≥† нМРлЛ®лРЬлЛ§. мЛЭ (9)мЧР к∞Б нХілєИмЭШ нПЙкЈ† нХілєИк≤љмВђл•Љ м†БмЪ©нХШк≥† fмЭШ нПЙкЈ†к∞ТмЭЄ 1.18мЭД мЈ®нХШл©і к∞Б нХілєИмЭШ мґХм≤Щк≥ДмИШмЭЄ A л•Љ кµђнХ† мИШ мЮИлЛ§ кЈЄл¶ђк≥† Table 2л°ЬлґАнД∞ кµђнХімІД Aк∞ТмЧР нХілЛєнХШлКФ м§СмХЩ мЮЕк≤љ D50л•Љ кµђнХЬ к≤∞к≥Љл•Љ м†ЬмЛЬнХШл©і Table 4мЩА к∞ЩлЛ§. нММлЮС м°∞к±імЧР лСФк∞РнХШк≥† м†Дл∞Шм†БмЭЄ нХілєИмЭШ нКємД±мЭД мЮШ л∞ШмШБнХШлКФ нХілєИ к≤љмВђк∞А нХілєИ нКємД±мЭШ лМАнСЬмД±мЭД к∞ЦлКФлЛ§к≥† л≥імХШмЭД лХМ мЭіл†Зк≤М мґФмВ∞нХЬ м§СмХЩ мЮЕк≤љмЭА мЮ•кЄ∞к∞Д нПЙкЈ†лРЬ мЮЕк≤љ м†Хл≥іл•Љ м†Ьк≥µнХ† к≤ГмЬЉл°Ь нМРлЛ®лРЬлЛ§.
Results of parameter f at survey sites
Dean(1977)мЭШ нПЙнШХнХілєИлЛ®л©і мЭіл°†мЛЭмЬЉл°ЬлґАнД∞ мЦїмЭА мЛЭ (11) лШРлКФ мЛЭ (12)лКФ Yates et al.(2009)мЧРмДЬ мИШнЦЙнХЬ мЮ•мЛЬк∞ДмЭШ кіАмЄ°мЭі мЧЖмЭілПД кЄ∞м°і л™®лЛИнД∞лІБ мЮРл£МмЭЄ м§СмХЩ мЮЕк≤љмЭілВШ нХілєИ к≤љмВђл°ЬлґАнД∞ мІБм†С мЗДнММлРШлКФ м†РмЧРмДЬмЭШ нММлЮС мЧРлДИмІАл•Љ мХИлЛ§л©і нХімХИмД†мЭі мЦілЦїк≤М мИШл†інХШк≤М лРШлКФ мІАл•Љ нММмХЕ нХ† мИШ мЮИлКФ к∞ДнОЄнХЬ мИШлЛ®мЭі лРЬлЛ§. Table 5лКФ Yates et al.(2009)мЭШ кіАмЄ° мЮРл£Мл°ЬлґАнД∞ мЦїмЭА к≤∞к≥Љл°ЬмДЬ мЛЭ (1)мЭШ aмЩА мЛЭ (11)мЭШ кЈЉмВђ нХімЭЄ a к≤∞к≥Љл•Љ мДЬл°Ь лєДкµРнХЬ к≤ГмЭілЛ§. мЛЭ (11)мЧРмДЬ оГ•лКФ мИШмЛђмЧР лФ∞лЭЉ мХљк∞ДмЭШ л≥АнЩФл•Љ л≥імЭілКФ лН∞ Table 5мЭШ к≤∞к≥ЉлКФ мИШмЛђ 3mмЧР лМАнХЬ к≤∞к≥Љл•Љ м†ЬмЛЬнХЬ к≤ГмЭілЛ§.
Torrey Pines нХіл≥Ак≥Љ Camlp Pendleton нХіл≥АмЭШ к≤љмЪ∞ нХілєИк≤љмВђ мЮРл£Мл°ЬлґАнД∞ мЦїмЭА к≤∞к≥Љк∞А лНФ кЈЉм†СнХЬ к≤∞к≥Љл•Љ м†ЬмЛЬнХШк≥† мЮИмЬЉлВШ Cardiff нХіл≥АмЭШ к≤љмЪ∞лКФ MSLмЧРмДЬ кіАмЄ°лРЬ м§СмХЩмЮЕк≤љ мЮРл£Мл°ЬлґАнД∞ мЦїмЭА к≤∞к≥Љк∞А лНФ кЈЉм†СнХЬ к≤∞к≥Љл•Љ л≥імЭік≥† мЮИлЛ§. мЧђкЄ∞мДЬ мЬ†лЕРнХ† к≤ГмЭА кіАмЄ°лРЬ aк∞ТмЭА мИШмЛђ 10mмЧРмДЬ кіАмЄ°лРЬ нММлЮС мЧРлДИмІАл°ЬлґАнД∞ мЦїмЦімІД к≤∞к≥ЉмЭіл©∞ к≥ДмВ∞лРЬ aлКФ мЗДнММм†РмЧРмДЬмЭШ нММлЮС мЧРлДИмІАл°ЬлґАнД∞ мґФмґЬнХЬ к≤ГмЭілЛ§. м∞Єк≥†л°Ь мИШмЛђ 10mмЧРмДЬ м£ЉкЄ∞ 6міИмЭЄ нММлЮСмЭШ нММлЮС мЧРлДИмІАк∞А 0.2m2мЭЄ к≤љмЪ∞ 10m мІАм†РмЬЉл°ЬлґАнД∞ мЗДнММм†РкєМмІАмЭШ м≤ЬмИШк≥ДмИШлКФ мХљ 1.13мЭі лРЬлЛ§.
мЛЭ (6)мЭД мЭімЪ©нХШл©і мЬ†мЮЕлРШлКФ нММлЮС мЧРлДИмІАл≥Дл°Ь нХімХИмД†мЭі мЦілЦїк≤М л∞ШмЭСнХШлКФ мІАл•Љ мВінОіл≥Љ мИШ мЮИлЛ§. мЛЭ (6)мЧР м£ЉмЦімІД мЗДнММм†РмЧРмДЬмЭШ нММк≥†л•Љ мИШмЛђ 10mмЧРмДЬмЭШ нММк≥†л°ЬмЭШ л≥АнЩШмЭД мЬДнХШмЧђ м°∞мДЭмЭШ мШБнЦ•мЭА лђімЛЬнХШк≥† м≤ЬмИШ нЪ®к≥Љл•Љ л∞ШмШБнХШмШАлЛ§. нММнЦ• мЮРл£Мк∞А мЧЖлКФ кіАк≥Дл°Ь кµім†ИмЭА лђімЛЬлРШмЧИлЛ§. Fig. 5лКФ Torrey Pines нХіл≥АмЧР лМАнХЬ к≤∞к≥Љл°ЬмДЬ Fig. 3к≥Љ к∞ЩмЭА м°∞к±імЧР лМАнХШмЧђ м†БмЪ©нХЬ мЛЭ (8)мЭШ к≤∞к≥ЉмЭілЛ§. нХілєИк≤љмВђ mмЭА нПЙкЈ†к∞ТмЭЄ 50мЬЉл°Ь к∞Дм£ЉнХШмШАмЬЉлВШ Table 5мЧР м£ЉмЦімІД л∞ФмЩА к∞ЩмЭі мґХм≤Щк≥ДмИШлКФ 2к∞АмІА к∞ТмЧР лМАнХШмЧђ м†БмЪ©лРШмЧИлЛ§. м¶Й, MSLмЧРмДЬ м±ДмЈ®нХЬ л™®лЮШмЭШ м§СмХЩмЮЕк≤љмЭД мВђмЪ©нХШмЧђ мЦїмЭА A=0.109m1/3мЭШ к≤љмЪ∞мЩА m=50мЬЉл°ЬлґАнД∞ мЛЭ (10)мЭШ кіАк≥Дл•Љ мЭімЪ©нХЬ мЦїмЭА A =0.0818m1/3мЭШ к≤љмЪ∞мЭілЛ§. нЫДмЮРмЭШ к≤љмЪ∞ кіАмЄ° к≤∞к≥ЉмЩА мЬ†мВђнХЬ к≤∞к≥Љл•Љ л≥імЭік≥† мЮИмЬЉлВШ м†ДмЮРмЭШ к≤љмЪ∞лКФ нХілєИк≤љмВђмЧР лєДнХШмЧђ м§СмХЩмЮЕк≤љмЭі нБђк≤М кіАмЄ°лРШмЦімДЬ Table 5мЭШ Observed aмЧР м†ЬмЛЬлРЬ ¬±2.0 мЭШ мШ§м∞® л≤ФмЬД лВімЧР лЖУмЭімІА л™їнХЬ к≤ГмЬЉл°Ь нМРлЛ®лРЬлЛ§. мИШмЛђ 1~2mмЧРмДЬ кіАмЄ°лРЬ м§СмХЩмЮЕк≤љмЭА MSLмЧР лєДнХШмЧђ мЮСмЭА мЮЕк≤љмЭЄ 0.18mmмЭЄ к≤ГмЬЉл°Ь кіАмЄ°лРШмЧИмЬЉлВШ MSLмЧРмДЬ лМАм≤іл°Ь нБ∞ мЮЕк≤љмЭД л≥імЭілКФ к≤љнЦ•мЭі мЮИлЛ§лКФ м†РмЭД к≥†л†§нХШл©і мХДмІБлПД л≥Є мЧ∞кµђмД±к≥Љл•Љ лІМм°±мЛЬнВ§мІА л™їнХШлКФ кіАмЄ° к≤∞к≥ЉмЭЄ к≤ГмЬЉл°Ь нМРлЛ®лРЬлЛ§.
Cardiff нХіл≥АмЧР лМАнХімДЬлКФ нХілєИ к≤љмВђ mмЭД нПЙкЈ† нХілєИ к≤љмВђ к∞ТмЭЄ 33.3мЬЉл°Ь м†БмЪ©нХШк≥† мЦїмЭА к≤∞к≥Љк∞А Fig. 6мЧР лПДмЛЬлРШмЧИлЛ§. Torrey Pines нХіл≥Ак≥Љ лІИм∞ђк∞АмІАл°Ь мґХм≤Щ к≥ДмИШлКФ 2к∞АмІА к∞ТмЧР лМАнХШмЧђ м†БмЪ©лРШмЧИлЛ§. м¶Й, MSLмЧРмДЬ м±ДмЈ®нХЬ л™®лЮШмЭШ м§СмХЩмЮЕк≤љмЭД мВђмЪ©нХШмЧђ мЦїмЭА A =0.0872m1/3мЭШ к≤љмЪ∞мЩА m=33.3мЬЉл°ЬлґАнД∞ мЛЭ (10)мЭШ кіАк≥Дл•Љ мЭімЪ©нХШмЧђ мЦїмЭА A =0.1073m1/3мЭШ лСРк∞АмІА к≤љмЪ∞мЭілЛ§. Torrey Pines нХіл≥Ак≥Љ лЛђл¶ђ м†ДмЮРмЭШ к≤љмЪ∞ кіАмЄ° к≤∞к≥ЉмЩА лєДкµРм†Б мЬ†мВђнХЬ к≤∞к≥Љл•Љ л≥імЭік≥† мЮИмЬЉлВШ нЫДмЮРмЭШ к≤љмЪ∞лКФ нХілєИк≤љмВђмЧР лєДнХШмЧђ м§СмХЩмЮЕк≤љмЭі мЮСк≤М кіАмЄ°лРШмЦімДЬ Table 5мЭШ Observed aмЧР м†ЬмЛЬлРЬ ¬± 1.0мЭШ мШ§м∞® л≤ФмЬД лВіл°Ь лУ§мЦімШ§мІА л™їнЦИлЛ§.
Camp Pendleton нХіл≥АмЧР лМАнХімДЬлПД Cardiff нХіл≥Ак≥Љ к∞ЩмЭі нХілєИ к≤љмВђ mмЭД 33.3мЬЉл°Ь м†БмЪ©нХШмШАлЛ§. Fig. 7мЧР кЈЄ к≤∞к≥Љк∞А лПДмЛЬлРШмЧИлЛ§. MSLмЧРмДЬ м±ДмЈ®нХЬ л™®лЮШмЭШ м§СмХЩмЮЕк≤љмЭД мВђмЪ©нХШмЧђ мЦїмЭА A =0.10m1/3мЭШ к≤љмЪ∞мЩА m=33.3мЬЉл°ЬлґАнД∞ мЦїмЭА A =0.1073m1/3мЭШ к≤љмЪ∞мЭілЛ§. Torrey Pines нХіл≥Ак≥Љ лІИм∞ђк∞АмІАл°Ь нЫДмЮРмЭШ к≤љмЪ∞ кіАмЄ° к≤∞к≥ЉмЩА мҐА лНФ мЬ†мВђнХЬ к≤∞к≥Љл•Љ л≥імЭік≥† мЮИмЬЉл©∞ м†ДмЮРмЭШ к≤љмЪ∞лКФ нХілєИк≤љмВђмЧР лєДнХШмЧђ м§СмХЩмЮЕк≤љмЭі мЮСк≤М кіАмЄ°лРШмЦімДЬ Table 5мЭШ Observed aмЧР м†ЬмЛЬлРЬ ¬±1.7мЭШ мШ§м∞® л≤ФмЬД лВіл°Ь лУ§мЦімШ§мІА л™їнЦИлЛ§. кЈЄлЯђлВШ мИШмЛђ 1~2mмЧРмДЬ кіАмЄ°лРЬ м§СмХЩмЮЕк≤љмЭі MSLмЧР лєДнХШмЧђ нЫ®мФђ нБ∞ к≤ГмЭД к∞РмХИнХШл©і л≥Є мЧ∞кµђ мД±к≥Љл•Љ мґ©лґДнЮИ лІМм°±мЛЬнВђ мИШ мЮИлКФ нХіл≥А м°∞к±імЭД к∞ЦмґШ к≤ГмЬЉл°Ь нМРлЛ®лРЬлЛ§.
мЭімГБмЭШ к≤∞к≥Љл•Љ мҐЕнХ©нХШл©і Dean(1977)мЭШ нПЙнШХнХілєИлЛ®л©імЛЭмЭД мЭімЪ©нХШмЧђ мЬ†мЮЕнММлЮС мЧРлДИмІА лШРлКФ мЬ†мЮЕнММк≥†л°ЬлґАнД∞ нХімХИмД†мЭі л∞ШмЭСнХШлКФ к≤ГмЭД мЖРмЙљк≤М мШИмЄ°нХ† мИШ мЮИмЬЉл¶ђлЭЉ нМРлЛ®лРЬлЛ§. мґХм≤Щк≥ДмИШ лШРлКФ м§СмХЩмЮЕк≤љмЭі мї§мІИмИШл°Э нХімХИмД†мЭШ л∞ШмЭСмЭА лСФнЩФлРШл©∞ нХілєИ лЛ®л©і нКємД±мЭД к≤∞м†ХнХШлКФ мґХм≤Щк≥ДмИШмЩА нХілєИк≤љмВђ к∞ДмЭШ л∞Ам†СнХЬ мГБкіАкіАк≥Дк∞А м°імЮђнХ† к≤ГмЬЉл°Ь нМРлЛ®лРЬлЛ§. мЛЭ (6)мЭД м†БмЪ©нХШлКФ к≤љмЪ∞ мЛЭ (11) лШРлКФ мЛЭ (12)л°ЬлґАнД∞ мІБм†С нХімХИмД†мЭШ мГБкіАк≥ДмИШ aл•Љ мЦїмЭА к≤∞к≥ЉмЩА лєДкµРнХШмЧђ мЧРлДИмІАмЩА нХімХИмД†мЭШ мГБкіАк≥ДмИШл•Љ нЖµнХШмЧђ мШИмЄ°нХЬ к≤∞к≥ЉмЩА мЬ†мВђнХЬ к≤љнЦ•мЭД л≥імЭік≥† мЮИлЛ§. кЈЄлЯђлВШ мЛЭ (6)мЭА нПЙкЈ†нММк≥†л≥ілЛ§ мЮСмЭА нММлЮСмЭі мЬ†мЮЕнХШлКФ к≤љмЪ∞ нХімХИмД†мЭі мШ§нЮИ놧 мЭМмИШмЭШ Seqл•Љ л≥імЭіл©∞ мє®мЛЭлРШлКФ к≤∞к≥Љл•Љ л≥імЭік≥† мЮИмЦі мЭімЧР лМАнХШмЧђ нЦ•нЫД нШДмЮ• мЮРл£МмЩАмЭШ лєДкµРл•Љ нЖµнХШмЧђ нЩХмЭЄмЭі нХДмЪФнХШлЛ§. лЛємЮ• мЭілЯђнХЬ лђЄм†Ьм†РмЭА мЛЭ (6)мЭД мІБм†С мЭімЪ©нХШлКФ к≤ГмЭі мХДлЛИлЭЉ мЛЭ (8)мЭД м†БмЪ©нХШл©і нХік≤∞лР† мИШ мЮИлЛ§. кЈЄлЯђлВШ нЦ•нЫД нШДмЮ• кіАмЄ°мЭД нЖµнХШмЧђ м†АнММлЮСмЭі мЬ†мЮЕлРШлКФ к≤љмЪ∞лКФ лђЉл°† м†Дл∞Шм†БмЬЉл°Ь л≥Є лЕЉлђЄмЧРмДЬ м†ЬмЛЬнХЬ к∞ЬлЕРмЭШ нГАлЛємД±мЭі нЩХмЭЄлР† нХДмЪФмД±мЭА мЮИлЛ§.
л≥Є мЧ∞кµђмЧРмДЬлКФ лѓЄкµ≠ мЇШл¶ђнПђлЛИмХД нХіл≥АмЧРмДЬ мИШнЦЙлРЬ Yates et al.(2009)мЭШ нШДмЮ•кіАмЄ° мЛ§нЧШ к≤∞к≥Љл°ЬмДЬ мЦїмЭА мЬ†мЮЕнММлЮС мЧРлДИмІАмЩА мИШл†інХімХИмД†мЬДмєШмЩАмЭШ мГБкіАкіАк≥Д к≥ДмИШлУ§мЭШ нОЄл¶ђнХЬ мґФм†ХмЭД мЬДнХШмЧђ Dean(1991)мЭШ нПЙнШХнХілєИлЛ®л©імЭШ мґХм≤Щк≥ДмИШAмЩА нПЙкЈ†нХілєИлЛ®л©і к≤љмВђmмЬЉл°ЬлґАнД∞ мЬ†мЮЕ нММлЮС мЧРлДИмІАмЩА мИШл†і нХімХИмД†к∞ДмЭШ к∞ДлЛ®нХЬ кіАк≥ДмЛЭмЭД м†ЬмЛЬнХШмШАлЛ§. мЭі мЛЭмЭШ к≤∞к≥ЉлКФ Yates et al.(2009)мЭШ 3мІАм†РмЧРмДЬ м†ЬмЛЬлРЬ мГБкіАкіАк≥Д к≥ДмИШмЩА лєДкµРлРШмЧИмЬЉл©∞ лМАм≤іл°Ь лІМм°±нХ†лІМнХЬ к≤∞к≥Љл•Љ мЦїмЧИлЛ§. лШРнХЬ Yates et al.(2009)мЭШ мЛ§нЧШ к≤∞к≥Љл°ЬлґАнД∞ нПЙнШХнХілєИлЛ®л©імЭШ мґХм≤Щк≥ДмИШ AмЩА нПЙкЈ†нХілєИлЛ®л©і к≤љмВђ mк∞ДмЭШ кіАк≥Дл•Љ лґДмДЭнХШмШАмЬЉл©∞ мЭі к≤∞к≥Љл•Љ мЭімЪ©нХШмЧђ мЬ†мЮЕнММлЮС мЧРлДИмІАмЧР лѓЉк∞РнХЬ м§СмХЩмЮЕк≤љл≥ілЛ§ лСФк∞РнХЬ нХілєИлЛ®л©ік≤љмВђл•Љ мЭімЪ©нХШл©і YatesмЭШ к≤∞к≥ЉмЩА мҐА лНФ мХИм†Хм†БмЭіл©імДЬлПД мЬ†мВђнХЬ к≤∞к≥Љл•Љ лВ≥лКФ к≤ГмЬЉл°Ь лґДмДЭлРШмЧИлЛ§.
лФ∞лЭЉмДЬ Yates et al.(2009)к≥Љ к∞ЩмЭА нШДмЮ•кіАмЄ° мЛ§нЧШмЭД мИШнЦЙнХШмІА мХКмХДлПД нЪ°лЛ®нСЬмВђл°ЬлґАнД∞ л∞ЬмГЭнХШлКФ нХімХИмД†мЭШ м†ДмІД л∞П нЫДнЗі к≤љнЦ•мЭД мЬ†мЮЕнХШлКФ нММлЮС мЧРлДИмІАмЭШ нХ®мИШл°Ь мЙљк≤М мґФм†ХнХ† мИШ мЮИлКФ л∞©л≤ХмЭЄ к≤ГмЬЉл°Ь нПЙк∞АлРШл©∞, нКєнЮИ к≥†нММлЮС лВімКµмЬЉл°Ь мЭЄнХЬ нХімХИмє®мЛЭмЭД мЩДнЩФнХШкЄ∞ мЬДнХЬ лМАнСЬм†БмЬЉл°Ь нХімХИкµђм°∞лђЉмЭЄ мЮ†м†Ь л∞П мЭімХИм†ЬмЭШ мє®мЛЭм†Ак∞Р кЄ∞лК• мД§к≥ДмЧРлПД м§СмЪФнХЬ м†Хл≥іл•Љ м†Ьк≥µнХ† мИШ мЮИлКФ к≤ГмЬЉл°Ь нМРлЛ®лРЬлЛ§. нЦ•нЫД кµ≠лВімЭШ нХімХИмД† л™®лЛИнД∞лІБ мЮРл£МмЩА нХілєИ лЛ®л©і л™®лЛИнД∞лІБ мЮРл£Мл•Љ м†БмЪ©нХШмЧђ мҐА лНФ м†Хл∞АнХЬ лєДкµР л∞П к≤Ам¶ЭмЭі нХДмЪФнХ† к≤ГмЬЉл°Ь мВђл£МлРЬлЛ§.
нЫДкЄ∞
л≥Є мЧ∞кµђлКФ нХімЦСмИШмВ∞лґАмЭШ вАЬмЧ∞мХИмє®мЛЭ м†Ак∞РкЄ∞мИ† к∞Ьл∞ЬвАЭ мД±к≥Љ м§С мЭЉлґАмЭіл©∞, гИЬлМАмШБмЧФмІАлЛИмЦілІБмЭШ вАЬмє®мЛЭм†Ак∞Р нХімХИкµђм°∞лђЉмЭШ л∞∞мєШмД§к≥Д мЧ∞кµђвАЭмЭШ мЧ∞кµђлєД мІАмЫРк≥Љ к≥µлПЩ лЕЉмЭШ к≤∞к≥Љл°Ь кµђм≤ім†Б мД±к≥Љл•Љ мЭіл£®мЧИмЭМмЭД л∞ЭнЮИл©∞ мЧ∞кµђлєД мІАмЫРмЧР к∞РмВђлУЬл¶љлЛИлЛ§.
Fig. 3.
Mean sea level(MSL) changing rate w.r.t. incident wave energy in Torrey Pines Beach (Yates et al., 2009)

Fig. 5.
Comparison between observed and predicted MSL changing rates for Torrey Pines beach (A unit : m1/3)

Fig. 6.
Comparison between observed and predicted MSL changing rates for Cardiff beach (A unit : m1/3)

Fig. 7.
Comparison between observed and predicted MSL changing rates for Camp Pendleton beach (A unit : m1/3)
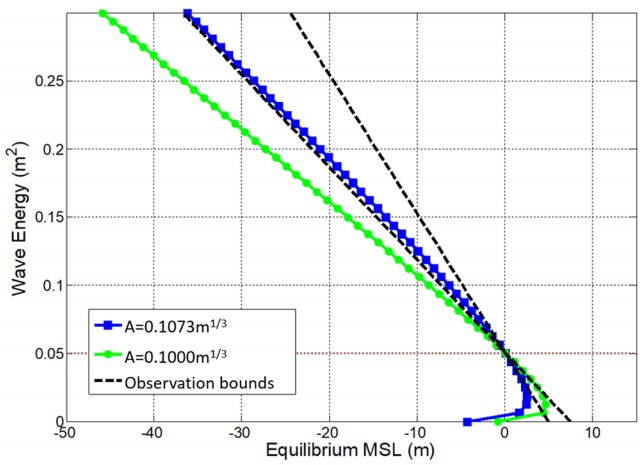
Table 1.
General beach characteristic of survey sites (Yates et al., 2009)
Table 2.
Scale factors according to median grain size (Dean et al., 1977)
Table 4.
Results of D50 estimated from the beach slopes
Table 5.
Comparison of correlation curve slope a for survey sites
References
Bruun, P. (1954). Coastal Erosion and Development of Beach Profiles. Technical Memorandum No. 44, US Army Corps of Engineers: Washington, D.C.
Bruun, P. (1962). Sea-Level Rise as a Cause of Shore Erosion. Journal of the Waterways and Harbors Division, 88(1), 117-132.

Cheon, SH., & Ahn, KM. (2008). Numerical Simulation of Beach Profile Changes. Journal of Korean Society of Coastal and Ocean Engineers, 20(1), 101-109.
Dean, RG. (1977). Equilibrium Beach Profiles: U.S. Atlantic and Gulf Coasts. Technical Report No. 12, Department of Civil Engineering, University of Delaware.
Dean, RG. (1991). Equilibrium Beach Profiles: Characteristics and Applications. Jounal of Coastal Research, 7(1), 53-84.

Dean, RG., Walton, TL., & Kriebel, DL. (2001). Cross-shore sediment transport. Coastal Engineering Manual. U.S. Army Coastal and Hydraulics Laboratory.
Kim, DS., & Lee, KL. (2015). Seasonal Changes of Shorelines and Beaches on East Sea Coast, South Korea. Journal of the Korean Geographical Society, 50(2), 147-164.
Kriebel, DL., & Dean, RG. (1993). Convolution Method for Time-Dependent Beach Profile Response. Journal of Waterway, Port, Coastal Ocean Engineering, 119(2), 204-226.

Larson, M., & Kraus, NC. (1989). SBEACH: Numerical Model for Simulating Storm-Induced Beach Change - Report 1 Empirical Foundation and Model Development. Technical Report, CERC-89-9, US Army Corps of Engineering.
Lee, JL., & Kim, IH. (2006). A Survey and Analysis of Swim Zone Width and Beach Scale Factor for Gangwon Beaches. Journal of Korean Society of Coastal and Ocean Engineers, 18(3), 241-250.
Miche, R. (1944). Mouvement Ondulatoires De La Mer en Profondeur Constante ou Decroissante. Annales de Ponts et Chaussees.
Miller, JK., & Dean, RG. (2004). A Simple New Shoreline Change Model. Coastal Engineering, 51(7), 531-556.

Moor, BD. (1982). Beach profile evolution in response to changes in water level and wave height. MCE Thesis, Department of Civil Engineering, University of Delaware; 164.
Park, JC., Han, KM., & Kim, JJ. (1993). A Study on the Numerical Model for Predicting Shoreline Changes. Journal of Ocean Engineering and Technology, 7(1), 156-161.
Plant, NG., Holman, RA., & Freilich, MH. (1999). A Simple Model for Interannul Sandbar Behavior. Journal of Geophys. Res, 104(C7), 15755-15776.

Son, CB. (1993). Prediction of Potential Shoreline Retreat by Sea Level Rise. Journal of Korean Society of Coastal and Ocean Engineers, 11(1), 34-40.
Son, CB., & Lee, SK. (2000). An Experimental Study on the Shoreline Change during Beach Process. Journal of Ocean Engineering and Technology, 14(3), 55-60.
- TOOLS
-
METRICS

-
- 8 Crossref
- Scopus
- 7,196 View
- 113 Download
- Related articles in JOET
-
Analysis of Impulse Turbine for Wave Energy Conversion Using CFD Method2004 October;18(5)